QC検定2級 抜取検査

勉強法

計数規準型抜取検査が頻出のため抑える．
特に，生産者危険や消費者危険，OC曲線の意味や振る舞い(サンプル数$n$や合格判定個数$c$を変化させたときに概形がどうなるか)をイメージできるようにする．

QC検定2級 他の記事

QC検定2級に関して、他の学習事項についても下記にまとめている。

単元	難易度
重要語句(実践編)	1
重要語句(手法編)	2
信頼性工学	1
管理図	2
抜取検査	2
検定/推定 回帰分析	3
実験計画法	3

抜取検査

• 抜取検査：ロットの中からサンプルを取り出し不適合品の数を数え，その数によってロットの合否を決める検査
• 抜取検査の採用条件
  • ロット数が決まっていること
  • 不適合品の混入が許されること
• 抜き取り検査の種類
  • 計数値抜取検査：不適合品の数を数え、許容の個数以下であるかを確認する
  • 計量値抜取検査：サンプルの計量値データから平均と標準偏差を計算し、判定基準と比較する

計数規準型抜取検査

• ロットの合格・不合格を，抜き取ったサンプル中の不適合品の数を数え、許容の個数以下であるかで判定する検査
• サンプル数と合格判定個数は，次の生産者危険（一般的に$\alpha=0.05$）と消費者危険（一般的に$\beta=0.1$）を鑑みて、サンプルの大きさ$n$と合格判定個数$c$を決定する
• 生産者危険：品質の良いロットが不合格になる確率$\alpha$
• 消費者危険：品質の悪いロットが合格になる確率$\beta$
• 表で整理：帰無仮説$H_0$が「合格品」，対立仮説が「不合格品である」とする
  • 第1種の誤りが「本当は合格品なのに不合格と判断」となるので，生産者が不利益を被る　⇒　生産者危険
  • 第2種の誤りが「本当は不合格品なのに合格と判断」となるので，消費者が不利益を被る　⇒　消費者危険

	$H_0$を採択(合格と判断)	$H_1$を採択(不合格と判断)
本当は$H_0$(合格)	$1-\alpha$	$\alpha$
本当は$H_1$(不合格)	$\beta$	$1-\beta$

n,cの決め方

• OC曲線（検査特性曲線）
  • 検査で合格となる確率は、二項分布（またはポアソン分布）の累積関数になる
  • 横軸にロットの不適合率$p$、縦軸にロットの合格率$L(p)$をプロットした曲線（不適合率がx軸なので、単調減少のグラフ）
    
• 計数規準型一回抜取検査表：この表から，$p_0, p_1$の数値が決まれば，サンプル大きさ$n$と合格判定個数$c$が求められる
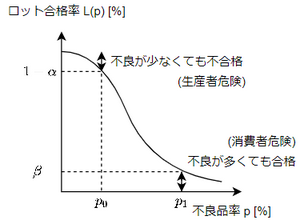
  • $p_0$：なるべく合格させたいロットの不適合率の上限
  • $p_1$：なるべく不合格にしたいロットの不適合率の下限
  • $p_0, p_1$は，OC曲線上で生産者危険$\alpha$(=0.05)と消費者危険$\beta$(=0.1)から求まる（図より必ず$p_0 < p_1$になる）

OC曲線の振る舞い

• $c$一定でサンプル数$n$を変化させた時
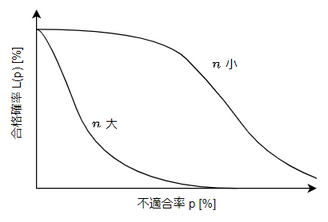
  • $n$が大きいと$c=0$（1つも不適合品が入ってはいけない）のときの合格率が極端に下がるはず
    
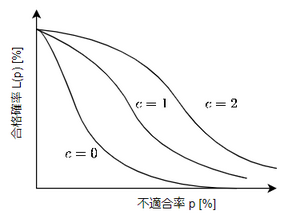
• $n$一定で合格判定個数$c$を変化させた時
  • $c$を増やすと当然合格確率は全体的に増える
    
• $n, c$一定でロット数$N$を変化させた時
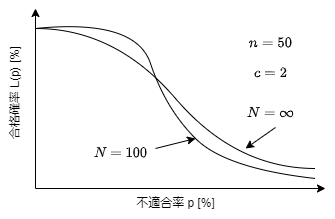
  • $N$が大きいと$c=0$（1つも不適合品が入ってはいけない）のときの合格率が下がるはず
    

計量規準型抜取検査

特性が計量値（測定で測れる）とき、正規分布を仮定し平均値と標準偏差から不適合数を求める検査のこと．

• 性質
• 手間が大きい（特性値を計測する必要があるため）
• 計数型よりもサンプル数は少なくて良い
• 手順
  1. 上限規格値$S_U$と下限規格値$S_L$、$p_0, p_1$を決める
  2. 抜取検査表からサンプル数$n$と合格判定計数$k$($\sigma$の何倍まで許容するか)を求める
  3. 上限規格値$S_U$と$\bar{x}+k\sigma$、下限規格値$S_L$と$\bar{x}-k\sigma$と比較し、合否判定する
• $\sigma$既知のときと$\sigma$未知で規格が異なるが、流れに大きな差異はない
  • JIS Z 9003 計量規準型抜取検査($\sigma$既知)
  • JIS Z 9004 計量規準型抜取検査($\sigma$未知)

参考文献

• 教科書（日本規格協会）

• 過去問題集（日本規格協会）