勉強法
マークシート方式のため、語句の暗記は必要ない。
それぞれの用語について、概要が思い浮かび、なぜその用語が重要かが分かる状態を目指す。
QC検定2級 他の記事
QC検定2級に関して、他の学習事項についても下記にまとめている。
QC7つ道具
特性要因図とパレート図,管理図は馴染みが少ないと思われるため,確認しておく.
管理図については,より詳細な内容が出題されるため,別ページに内容をまとめている.
→ https://www.kennzo.net/qc-kentei-2-control-chart
- グラフ
- 特性要因図
- 管理用の特性要因図:特性制御の要因を整理する図
- 解析用の特性要因図:工程異常の原因工程の特性をし、その原因工程について4Mや5Mの観点で要因を洗い出した図
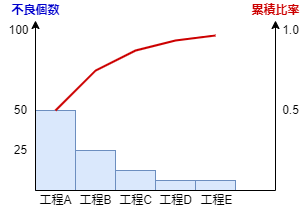
- パレート図:階級ごとの度数を大きい順に並べ,ヒストグラムと累積比率をプロットした図
- 重点課題の絞り込みに使用できる
- 例:横軸に工程、縦軸に不良品率を書き、問題のある工程の絞り込みができる
- ヒストグラム
- 散布図
- 管理図
- チェックシート
新QC7つ道具
前半の手法編で超頻出事項である.それぞれの概要や使いどころ,関連語句まで押さえておくと良い.
- 親和図法
- 概要:課題要因を親和性に基づきグループ分けした図
- 使い所:課題構造の明確化
- 連関図法
- 概要:因果関係を論理的に繋いだ図
- 使い所:要因が複雑に絡み合っているときの整理
- 系統図法
- 概要:目的達成するための手段をツリー状に配置した図
- 使い所:目的を達成する最適な手段を探したい時
- PDPC法(過程決定計画図:Process Decision Program Chart)
- 概要:ゴールまでのプロセスを示したチャート形式の図
- 使い所:ゴールまでに予想される障害の事前予測、および代替案の検討
- マトリックス図法
- 使い所:複数の要素間の関係を整理したいとき
- マトリックス・データ解析法
- 概要:数値データを2つの評価項目で散布図で描く(新7つ道具の中で唯一数値データを使う)
- 使い所:数値データの特徴把握
- アローダイアグラム
- 概要:実行する手順や日数を示した図
- 使い所:実行手順、日数の整理・削減検討
工程能力指数
工程能力指数(Process Capability Index)は、規定のばらつきに対して実際のばらつきがどの程度大きいかを表す指標である。
- 片側規格の場合
- 上限規格$S_U$だけがある場合:$C_{pU} = \frac{S_U – \bar{x}}{3s}$
- 下限規格$S_L$だけがある場合:$C_{pL} = \frac{\bar{x} – S_L}{3s}$
- 両側規格の場合
- 母平均が規格の中心にあるとできるとき:$C_p = \frac{S_U – S_L}{6s}$
- 母平均が規格の中心にあるとできないとき:$C_{pk} = \min{(C_{pU}, C_{pL})}$
評価基準
工程能力指数の値で範囲が示されることが多いが,それぞれ何$\sigma$程度であるかを押さえるのが分かりやすい。
6σ以下(片側なら3σ)は不足、あとは2σごと(片側なら1σごと)に「まずまず、十分、十分すぎる」となる
| 工程能力指数の範囲 | 意味(両側規格のとき) | 判断 |
|---|---|---|
| $C_p \ge 1.67$ | $S_U – S_L$ が$10\sigma$より大きい | 工程能力は十分すぎる |
| $1.67 > C_p \ge 1.33$ | $S_U – S_L$ が$8\sigma$〜$10\sigma$の間にある | 工程能力は十分である |
| $1.33 > C_p \ge 1.0$ | $S_U – S_L$ が$6\sigma$〜$8\sigma$の間にある | 工程能力は十分とは言えないがまずまず |
| $1.0 > C_p \ge 0.67$ | $S_U – S_L$ が$4\sigma$〜$6\sigma$の間にある | 工程能力は不足している |
| $0.67 > C_p$ | $S_U – S_L$ が$4\sigma$より小さい | 工程能力は非常に不足している |
確率分布
QC検定2級については,正規分布と二項分布,ポアソン分布を押さえておけばよい.
| 種類 | f(x) | 期待値 | 分散 |
|---|---|---|---|
| 正規分布 | $\frac{1}{\sqrt{2 \pi \sigma^2}} \exp{ \left(- \frac{(x-\mu)^2}{2\sigma^2} \right) }$ | $\mu$ | $\sigma$ |
| 二項分布 | $_nC_x p^x(1-p)^{1-x}$ | $np$ | $np(1-p)$ |
| ポアソン分布 | $\frac{\lambda^k}{k!} e^{-\lambda}$ | $np$ | $np$ |
サンプリングの種類
サンプリング手法は頻出のため,次の手法の違いはしっかり押さえる必要がある.
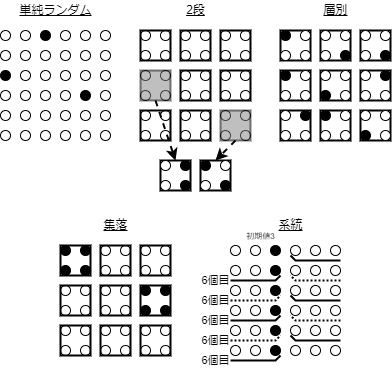
- 単純ランダムサンプリング:完全にランダムに抽出
- 2段(多段)サンプリング:無作為抽出を繰り返す手法
- 層別サンプリング:いくつかのグループ分けをしたあと,それぞれから無作為に選ぶ
- 例:男,女から○人選ぶ
- 集落(クラスター)サンプリング:母集団を網羅的に分割しクラスターを作り,その中からクラスターを抽出し,その構成員すべてを調査する手法
- 系統サンプリング:1つ目に選ぶデータを無作為に決め,そこから等間隔にデータを抽出する
参考文献
- 教科書(日本規格協会)
- 過去問題集(日本規格協会)
