今回は増幅器として最もシンプルな1段のソース接地回路ついて説明する.
ソース接地回路
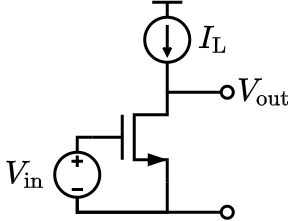
ソース接地回路とは次に示すようにソースが接地された増幅回路である.
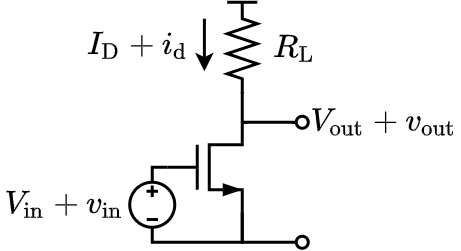
次の図は電流源を負荷としたソース接地回路である.
ソース接地回路は電圧利得が大きいため,電圧増幅段として頻繁に使用される.
小信号と大信号
上記の回路では入力には$V_{\rm in} + v_{in}$ の電圧が印加されていて,$V_ {\rm in}$ はバイアス電圧,$v_{\rm in}$ は信号成分である.
信号成分には様々な波形が考えられ得るが,正弦波として捉えるのが一番考えやすい.
電圧だけでなく図中の大文字で表している$V_{\rm in}$,$I_{\rm d}$,$V_{\rm out}$はバイアス点,すなわちDC成分であり,
小文字で表した$v_{\rm in}$,$i_{\rm d}$,$v_{\rm out}$は信号成分である.
増幅回路ではバイアス電圧を印加している状態(バイアス点)を中心に考えるのが一般的だ.
バイアス点は$v_{\rm in}= 0$ のときのことを示し,バイアス電圧$V_{\rm B}$ のみが印加され,一定電流$I_{\rm D}$ が流れている状態である.
それに加え,重要なのは交流成分$v_{\rm in}$の振幅の大きさである.
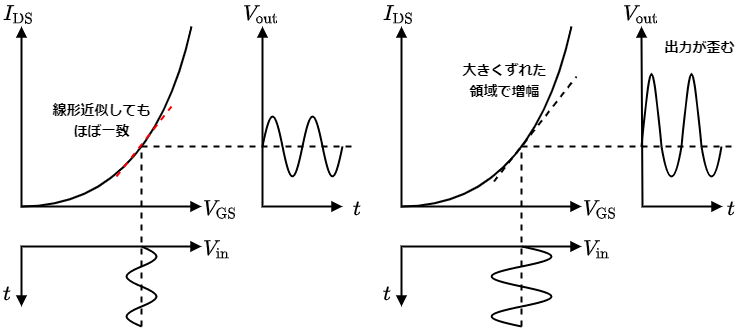
振幅が十分に小さいとき(小信号)は下の図のようにMOSFETの非線形性による歪みが小さく,相互コンダクタンスgmで線形近似しシンプルに考えることができる.
よって,バイアス点からの差分のみを考える小信号解析が適応できる.
一方で,振幅が大きいとき(大信号)はMOSFETの非線形性の影響が大きく,線形近似できない.
よって,小信号解析では正しい結果が得られない可能性がある.
以降では,入力信号が十分小さいとして小信号として話を進める.
電圧利得
電圧利得$A_{\rm v}$は電圧の増幅率であるが,その定義は
$$A_{\rm v} = \frac{v_{\rm out}}{v_{\rm in}}$$
で,すなわち信号成分の利得である.
以降ではこれについて説明する.
詳しい導出
ソース接地回路の電圧利得$A_{\rm v}$を詳しく見るために,まずは丁寧に回路方程式によって考える.
まず,出力電圧は
$$V_{\rm out} + v_{\rm out} = V_{\rm DD} – R_{\rm L}(I_{\rm D} + i_{\rm d})$$
となる.これをDC成分($V_{\rm in}$,$I_{\rm d}$,$V_{\rm out}$)と信号成分($v_{\rm in}$,$i_{\rm d}$,$v_{\rm out}$)で分けると
$$V_{\rm out} = V_{\rm DD} – R_{\rm L} I_{\rm D}$$
$$v_{\rm out} = -R_{\rm L} i_{\rm d}$$
がわかる.
また,MOSFETが飽和領域で動作しているとすると電流式は
$$I_{\rm D} = \frac{\beta}{2} (V_{\rm GS} – V_{\rm TH})^2$$
なので,今回の回路で当てはめると
$$I_{\rm D} + i_{\rm d} = \frac{\beta}{2} (v_{\rm in} + V_{\rm in} – V_{\rm TH})^2$$
となる.
これを簡単にするために$v_{\rm in}$について線形近似する.
$v_{\rm in}$についてマクローリン展開し,2次以降の項を無視すると
$$I_{\rm D} + i_{\rm d} \simeq \frac{\beta}{2} (V_{\rm in} – V_{\rm TH})^2 + \beta (V_{\rm in} – V_{\rm TH})v_{\rm in}$$
とできる.第二項は相互コンダクタンスを用いて
$$I_{\rm D} + i_{\rm d} \simeq \frac{\beta}{2} (V_{\rm in} – V_{\rm TH})^2 + g_{\rm m}v_{\rm in}$$
と表すことができる.
DC成分($V_{\rm in}$,$I_{\rm d}$,$V_{\rm out}$)と信号成分($v_{\rm in}$,$i_{\rm d}$,$v_{\rm out}$)で分けると
$$I_{\rm D} = \frac{\beta}{2}(V_{\rm in} – V_{\rm TH})^2$$
$$i_{\rm d} = g_{\rm m} v_{\rm in} $$
となる.
結局は,相互コンダクタンスの定義通り,信号成分$i_{\rm d}$は$v_{\rm in}$に対して線形に変化すると近似する考え方が重要になる.
上記の議論で,信号成分の関係式は
$$v_{\rm out} = -R_{\rm L} i_{\rm d}$$
$$i_{\rm d} = g_{\rm m} v_{\rm in}$$
なので,1式にまとめると
$$v_{\rm out} = -R_{\rm L} g_{\rm m} v_{\rm in}$$
になる.よって,電圧利得は
$$A_{\rm v} = \frac{v_{\rm out}}{v_{\rm in}} = -g_{\rm m}R_{\rm L}$$
とわかる.
よって,電圧利得を大きくするには$g_{\rm m}$又は$R_{\rm L}$を大きくすれば良い.
電圧利得の簡単な導出方法
上記のように丁寧に回路方程式から考えることで電圧利得が分かるが,もう少し簡単な方法がある.
電圧利得は$i_{\rm d}$を介すると次のように表せる.
$$A_{\rm v} = \frac{v_{\rm out}}{v_{\rm in}} = \frac{v_{\rm out}}{i_{\rm d}} \cdot \frac{i_{\rm d}}{v_{\rm in}} = R_{\rm out} g_{\rm m}$$
$R_{\rm out}$は小信号回路における出力抵抗である.
上記のソース接地回路では出力抵抗は$R_{\rm L}$なので
$$A_{\rm v} = g_{\rm m} R_{\rm L}$$
と一発でわかる.
実際は-がついているので符号は別途考える必要がある.
MOSFETのドレインソース間抵抗を考慮する場合
上記の回路でMOSFETのドレインソース間抵抗$r_{\rm ds}$を考慮する場合を考える.
このときの回路の出力抵抗は増幅に用いられるMOSFETの$r_{\rm ds}$とその他の負荷抵抗成分の並列抵抗で
$$R_{\rm out} = r_{\rm ds} // R_{\rm L}$$
となる.よって,電圧利得は
$$A_{\rm v} = g_{\rm m} \frac{r_{\rm ds} R_{\rm L}}{r_{\rm ds} + R_{\rm L}}$$
と分かる.
真性利得(intrinsic gain)
真性利得の説明をするために理想電流源を負荷とした場合,すなわち$R_{\rm L} = \infty$ の場合はどうなるかについて考える.
この時,出力抵抗は$R_{\rm out} = r_{\rm ds}$ となるので,電圧利得は
$$A_{\rm v} = g_{\rm m} r_{\rm ds}$$
となる.
負荷抵抗$R_{\rm L}$を$\infty$から小さくしていくと$R_{\rm out}$ も小さくなるため,この電圧利得$g_{\rm m} r_{\rm ds}$ は取り得る最大値になる.
また,このときの電圧利得は増幅しているMOSFETの特性のみで決定されており,MOSFET固有の定数となることが分かる.
よって,$R_{\rm L} = \infty$のときの電圧利得$g_{\rm m}r_{\rm ds}$ は真性利得(intrinsic gain)と呼ばれる.
まとめると,真性利得とは単体MOSFETが実現できる最大電圧利得$A_{\rm v} = g_{\rm m}r_{\rm ds}$と言える.
まとめ
増幅回路の電圧利得は
$$A_{\rm v} = \frac{v_{\rm out}}{v_{\rm in}} = \frac{v_{\rm out}}{i_{\rm d}} \cdot \frac{i_{\rm d}}{v_{\rm in}} = R_{\rm out} g_{\rm m}$$
と表せ,増幅段の$g_{\rm m}$と増幅器の出力抵抗から簡単に考えることができる.
よって,ソース接地回路の電圧利得は
$$A_{\rm v} = g_{\rm m} \frac{r_{\rm ds} R_{\rm L}}{r_{\rm ds} + R_{\rm L}}$$
となる.
また,真性利得は単体MOSFETが実現できる最大電圧利得であり,
$$A_{\rm v} = g_{\rm m} r_{\rm ds}$$
で表されるものである.
参考文献
[1] Behzad Razavi(2003),「アナログCMOS集積回路の設計」,丸善出版.
[2] LSI設計者のためのCMOSアナログ回路入門(2017),「LSI設計者のためのCMOSアナログ回路入門」,CQ出版社.