勉強法
語句はすべて頻出のため,意味や違いを抑える.
特に,「FMEA」など問題発生防止関連や「フェールセーフとフールプルーフの違い」,「バスタブ曲線などの故障率曲線」は頻出である.
計算問題としては,信頼度や故障率の計算は頻出のため,定義を理解しておく.
QC検定2級 他の記事
QC検定2級に関して、他の学習事項についても下記にまとめている。
信頼性とは
- ディペンダビリティ(Dependability):広義の信頼性
- 狭義の信頼性(故障しない):評価尺度は信頼度
- 保全性(故障しても修理可能):評価尺度は保全度
- アベイラビリティ(稼働率):修復時間/(修復時間+稼働時間)
- 信頼度(Rで表されることが多い):正常に動作する確率
- 保全度:保全作業が規定時間以内で終わる確率
問題の再発防止や未然防止
- 再発防止手法として、故障木解析(FTA:Fault Tree Analysis)
- 発生問題をツリーのトップとして原因分析
- 根本原因解析(RCA:Root Cause Analysis)の手法の一つ
- FT図(Fault Tree図):ANDやORの論理記号で故障原因と確率を表した図
- 未然防止手法として、故障モード影響解析(FMEA:Fault Mode and Effects Analysis)
- 故障モードをMECEに洗い出し、重要度を発生頻度や影響度で算出し、対策の必要性を決定する
耐久性
耐久性の尺度
- 平均故障寿命(MTTF:Mean Time To Failure):非修理系での製品の平均寿命
- 平均故障間隔(MTBF:Mean Time Between Failures):修理系での製品の平均寿命(修理期間の間の正常動作の期間)
- B10ライフ:10%が故障するまでの時間(故障分布関数F(T)=0.1となる時間)
- 故障率(λ):λ=1/MTBF
- 信頼度(R) :$R = e^{-\lambda t}$ 、故障率$\lambda$のときの故障確率分布は指数分布になる
- なぜ指数分布を用いるか?:指数分布は幾何分布において試行回数を無限回にすることで求められる分布、壊れるか壊れないかの試行を時間経過とともに常に行った確率と考える
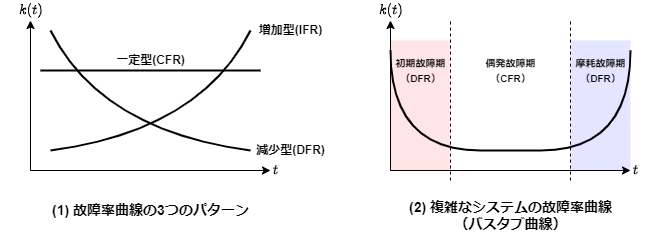
故障率曲線の典型例
- 初期故障期(DFR:Decreasing Failure Rate):出荷直後の時期は故障率が単調減少する
- 偶発故障期(CFR:Constant Failure Rate):故障率が一定の区間
- 摩耗故障期(IFR:Increasing Failure Rate):故障率が単調増加する期間、一般的にシステム劣化が原因
- バスタブ曲線:複雑なシステムの故障確率の時系列の曲線がバスタブ上になる、上記3つのグラフをかけ合わせたような曲線になるため
保全性
- 予防保全:故障の未然防止
- 時間計画保全:定期的に清掃(オーバーホール)する
- 状態監視保全:定期検査するオンコンディション方式(OC方式)、劣化検出するコンディション・モニタリング方式(CM方式)がある
- 事後保全:故障後に行う保全
- 修理時間の短さが重要
- 平均修復時間(MTTR:Mean Time To Repaire)
- アベイラビリティ(稼働率):修復時間MTBF/(修復時間MTTR+稼働時間MTBF)
- 設計信頼度
- フェールセーフ:故障時に致命的にならないようにする
- フールプルーフ(エラープルーフ):誤操作があっても安全性を保つ
- 信頼性モデル
- 信頼度R:正常に動作する確率
- 不信頼度F:故障確率1-R
- 直列系:信頼度R = R1×R2
- 並列系:信頼度R = 1 – (1-R1)(1-R2)
- m-out-of-n 冗長系:n個のうちm個動作してれば正常動作する
- 待機冗長系:使用中のものが故障したときは不使用のものを使う
参考文献
- 教科書(日本規格協会)
リンク
- 過去問題集(日本規格協会)
リンク
