MOSFETの相互コンダクタンス gm

アナログ回路を設計するうえで重要なパラメータとして相互コンダクタンス$ g_{\rm m} $があります．
この記事では$ g_{\rm m} $とは何なのかとその存在意義，さらにMOSFETにおけるの$ g_{\rm m} $の特性について説明します．

$ g_{\rm m} $の式変形はわかるけど物理的に何が起こっているか分からない…そんな方に是非読んでいただきたいです．

$ g_{\rm m} $の定義
1. $ g_{\rm m} $の存在意義
MOSFETの$ g_{\rm m} $
1. $ g_{\rm m} $を表す3つの式
$ g_{\rm m} $を表す3つの式の考え方
1. $ V_{\rm OV} $に対する$ g_{\rm m} $の変化
まとめ
参考文献

$ g_{\rm m} $の定義

$ g_{\rm m} $の定義は$ I_{\rm DS} $を$ V_{\rm GS} $で偏微分したもので

$$ g_{\rm m} = \frac{\partial I_{\rm DS}}{\partial V_{\rm GS}} $$

と表される．

$ g_{\rm m} $の存在意義

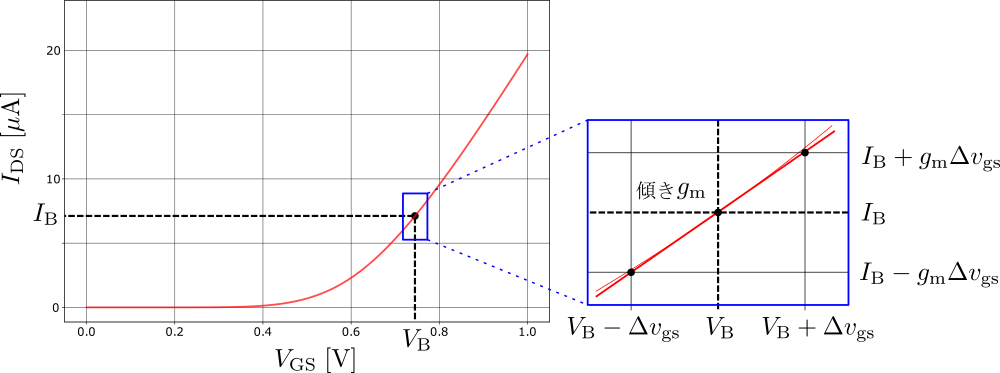
上式で$ g_{\rm m} $を定義したが，これは何の役に立つのか？という点を説明する．$ I_{\rm DS} – V_{\rm GS} $特性は下のグラフのようになる．

ここで， $ V_{\rm GS} = V_{\rm B} $とすると$ I_{\rm DS} – V_{GS} $特性のグラフから$ I_{\rm DS} = I_{\rm B} $の電流が流れる．

次は，$ V_{\rm GS} = V_{\rm B} + \Delta v_{\rm gs} $としてみる．
本来ならば$ I_{\rm DS} – V_{GS} $特性から読み取らなければならず具体的な数式で表すのが難しいが，$ g_{\rm m} $を用いると

$$ I_{\rm DS} = I_{\rm B} + g_{\rm m} \Delta v_{\rm gs} $$

のように線形に表すことができる．
これは視覚化すると下の図の拡大された部分である．

$ g_{\rm m} $を導入することで非線形なMOSFETの特性を一部の区間で線形近似することができる．

アンプなどアナログ信号を処理する場合は，直流成分(バイアス電圧)からどの程度変化したかで考え，まさに上のようにバイアス点を基準として線形近似して考える．
その変化分，上で言うと$ g_{\rm m} \Delta v_{\rm gs} $のみを考えることを小信号解析と言い，小信号解析で$ g_{\rm m} $がよく出てくるのはこのような理由がある．

MOSFETの$ g_{\rm m} $

MOSFETが飽和領域で動作しているときドレイン電流は

$$ I_{\rm DS} = K_{\rm n}’ \frac{W}{L} \left( V_{\rm GS} – V_{\rm TH} \right)^2 \label{eq:Ids_sat} $$

と表されるので，$ g_{\rm m} $の定義に従って$ I_{\rm DS} $を$ V_{\rm GS} $で偏微分すると

$$ g_{\rm m} =\frac{\partial I_{\rm DS}}{\partial V_{\rm GS}} = 2 K_{\rm n}’ \frac{W}{L} \left( V_{\rm GS} – V_{\rm TH} \right) \label{eq:gm} $$

となる．ここで，$ K_{\rm n}’ $は，

$$ K_{\rm n}’= \frac{\mu C_{\rm OX}}{2n} $$

で表され，nは $ n-1 = C_{\rm OX}/C_{\rm D} $ となる係数である．
$ C_{\rm OX} $は酸化膜，$ C_{\rm D} $は空乏層の容量である．
特に気にならない場合はMOSFET特有の定数があるんだぐらいでこの記事では問題ない．

一方，式\eqref{eq:Ids_sat}を$ V_{\rm GS} – V_{\rm TH} $と$ W/L $のそれぞれについて変形すると

$$ \label{eq:Vov} \left( V_{\rm GS} – V_{\rm TH} \right) = \sqrt{ \frac{I_{\rm DS}}{K_{\rm n}’ \frac{W}{L} }} $$ $$ \frac{W}{L} = \frac{I_{\rm DS}}{K_{\rm n}’ \left( V_{\rm GS} – V_{\rm TH} \right)^2} \label{eq:WL} $$

となる．
これらの式\eqref{eq:Vov}と\eqref{eq:WL}を式\eqref{eq:gm}に代入すると，次が得られる．

$$ g_{\rm m} = \sqrt{ K_{\rm n}’ \frac{W}{L} I_{\rm DS}}$$ $$ g_{\rm m} = \frac{2 I_{\rm DS}}{V_{\rm GS} – V_{\rm TH}} $$

こうして，$ g_{\rm m} $を表す式が3通りも出てきた．

$ g_{\rm m} $を表す3つの式

上記のように3つ$ g_{\rm m} $を表す式が出てきたが，これらの式は変数$ I_{\rm DS} , g_{\rm m}, V_{\rm GS} – V_{\rm TH}, W/L $の4変数を2つの式で整理したので2自由度である．

すなわち，これら3つの式の違いは$ I_{\rm DS} , V_{\rm GS} – V_{\rm TH}, W/L $のうちどの2つを変数としたかで$ g_{\rm m} $を表すことになる．
また，変数として選ばなかったあと1つのパラメータも自動的に決まることになる

では，このことを踏まえて上式をどれが変数かを明確にして書き直す．

$$ \label{eq:gm_LW_Vov} g_{\rm m} (\frac{W}{L}, V_{\rm OV}) = 2 K_{\rm n}’ \frac{W}{L} V_{\rm OV} $$ $$ g_{\rm m} (\frac{W}{L}, I_{\rm DS}) = \sqrt{ K_{\rm n}’ \frac{W}{L} I_{\rm DS}} $$ $$g_{\rm m} (I_{\rm DS}, V_{\rm OV}) = \frac{2 I_{\rm DS}}{V_{\rm OV}} \label{eq:gm_Ids_Vov} $$

見栄えを良くするために$ V_{\rm OV} =V_{\rm GS} – V_{\rm TH} $としている．
$ V_{\rm OV} $はOver-Voltageの頭文字をとっていて，字面通りゲートソース間電圧がしきい値電圧よりもどの程度大きいかを表す．

$ g_{\rm m} $を表す3つの式の考え方

友人か誰かに…

$ V_{\rm OV} $をでかくしたときに，$ g_{\rm m} $ってどうなんの？

と問われたとしよう．

式\eqref{eq:gm_LW_Vov}を見れば大きくなるんじゃないか

と答える．
しかし，おそらくそうすると

式\eqref{eq:gm_Ids_Vov}見たら反比例やし小さくなるのでは？そもそもこの式成立するの？

など色々反論されるだろう．
すなわち，式の見た目だけ見れば$ V_{\rm OV} $を変化させたときの$ g_{\rm m} $の変化が式\eqref{eq:gm_LW_Vov}と\eqref{eq:gm_Ids_Vov}で矛盾している．実はこれは2つの変数によって，$ g_{\rm m} $が変化するがもう1つの変数もそれに応じて変化している．
これを追えば上の疑問が解決されるのである．

$ V_{\rm OV} $に対する$ g_{\rm m} $の変化

式\eqref{eq:gm_LW_Vov}における挙動

まず，式\eqref{eq:gm_LW_Vov}で考えてみる．
$ \frac{L}{W}, V_{\rm OV} $が変数であるので，これらを決めれば残りの$ I_{\rm DS}, g_{\rm m} $も決まる．
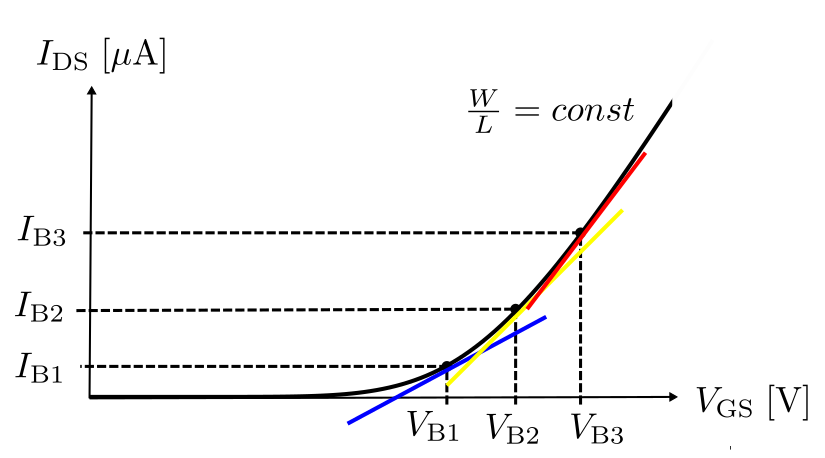
この2つの変数のうち一つを固定しないと考えにくいので，$ W/L $を固定して$ V_{\rm OV} $を動かしてみる．
これは次に示す$ I_{\rm DS} – V_{\rm GS} $で考えると，ただ単に$ V_{\rm GS} $を変化させているだけである．
グラフの傾きが$ g_{\rm m} $なので，$ I_{\rm DS} – V_{\rm GS} $を大きくすれば視覚的にも$ g_{\rm m} $が大きくなるのが把握できる(グラフ上で$ g_{\rm m} $の大小を青，黄，赤を用いて表現している)．

ここで，意識しておきたいのが$ I_{\rm DS} $である．
式\eqref{eq:gm_LW_Vov}で$ V_{\rm OV} $だけを動かしているつもりだったが，$ V_{\rm OV} $だけでなく意図せず式\eqref{eq:gm_LW_Vov}には出てきていない$ I_{\rm DS} $も大きく変化する点に注意である．

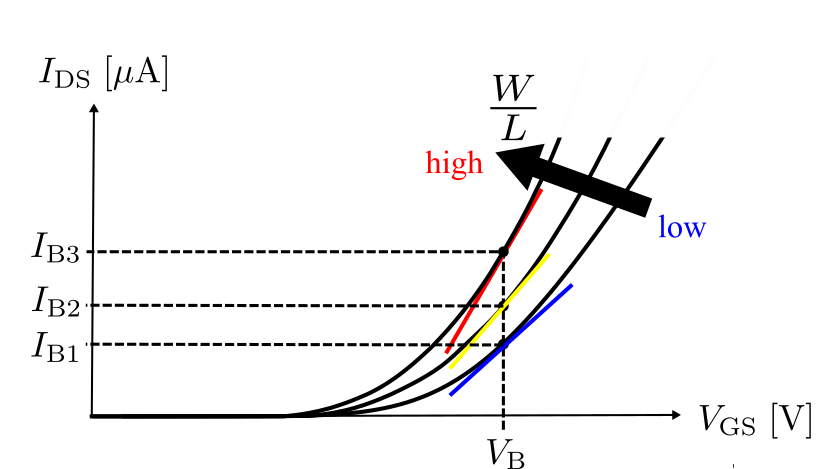
次に，同じく式\eqref{eq:gm_LW_Vov}で$ V_{\rm OV} $を固定して$ W/L $を動かしてみる．
これを$ I_{\rm DS} – V_{\rm GS} $グラフで考えると次のようになる．

$ W/L $を大きくすると矢印の方向に曲線が動くので，$ V_{\rm OV} $を一定にしていれば意図せず式\eqref{eq:gm_LW_Vov}に出現していない$ I_{\rm DS} $も大きくなる．
なので，$ W/L $を大きくすると$ g_{\rm m} $が大きくなる(同様にグラフ上で$ g_{\rm m} $の大小を青，黄，赤を用いて表現している)．

式\eqref{eq:gm_Ids_Vov}における挙動

それでは式\eqref{eq:gm_Ids_Vov}で考えてみる．
$ I_{\rm DS}, V_{\rm OV} $が変数であるので，これらを決めれば残りの$ W/L, g_{\rm m} $も決まる．
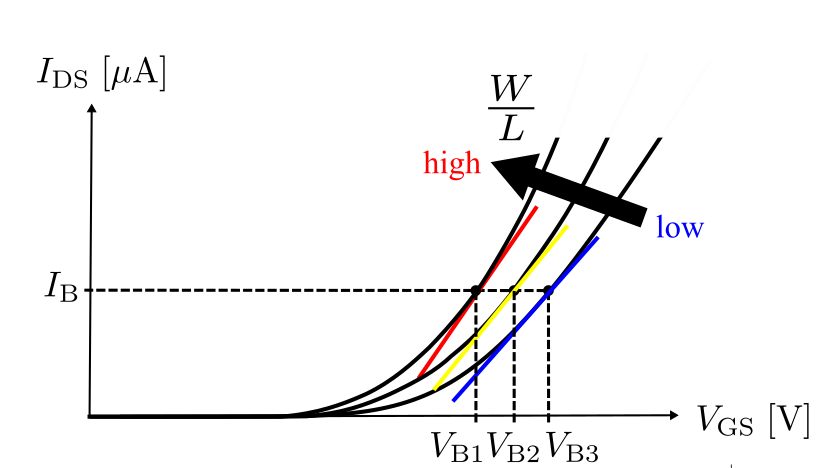
上記と同様にこの2つの変数のうち一つである$ I_{\rm DS} $を固定して$ V_{\rm OV} $を動かしてみる．
これを$ I_{\rm DS} – V_{\rm GS} $グラフで考えると次のようになる．
同じ$ V_{\rm OV} $を動かしているが，グラフで見れば式\eqref{eq:gm_LW_Vov}とは全く異なることが視覚的にわかると思う．
$ I_{\rm DS} $を固定して$ V_{\rm OV} $を増加させると，意図せず$ W/L $を小さくしていることになる
よって，$ g_{\rm m} $は小さくなるのである．

余談となるが，$ I_{\rm DS} $一定で逆に$ V_{\rm OV} $を小さくする(同時に$ W/L $を大きく，すなわちMOSFETを大きくしている)と$ g_{\rm m} $が大きくなる．
これは，消費電力を小さくしたい場合に重要な事実で，$ W/L $が大きい，サイズの大きいMOSFETで比較的低い$ V_{\rm GS} $で動作させれば低い消費電力で高いゲイン，すなわち$ g_{\rm m} $が得られる．
もちろん，サイズの大きいMOSFETを使っているので実装面積が大きくなるのが難点である．

また，$ V_{\rm OV} $を固定して$ I_{\rm DS} $を動かす場合は式\eqref{eq:gm_LW_Vov}で$ V_{\rm OV} $を固定して$ W/L $を動かしたとき(真ん中の図)と視覚的には変わらない．
もちろん，$ I_{\rm DS} $を大きくすると$ g_{\rm m} $は大きくなる．

まとめ

アナログ回路を設計もしくは勉強する上で$ g_{\rm m} $は極めて重要な設計パラメータとなる．
また，CMOSアナログ回路の場合はゲート長Lやゲート幅Wをある程度自由に変えられるので上の例でも述べたように同じ$ g_{\rm m} $をとる場合でも$ L, W $や $ V_{\rm OV}, I_{\rm DS}$の異なる組み合わせが多くある．
この中から用途に合わせた回路が設計できるかはまさにここら辺の知識が特に重要なので，皆様の理解の助けになればと思います．