MOSFETの原理と特性

この記事ではMOSFETの原理の説明と電流式の導出を行う．

MOSFET
1. 動作原理
2. ピンチオフ現象(MOSFETの電流が飽和する理由)
MOSFETの一般的な電流式の導出
1. ピンチオフ現象と電流飽和
空乏層容量を考慮した場合
まとめ
参考文献

MOSFET

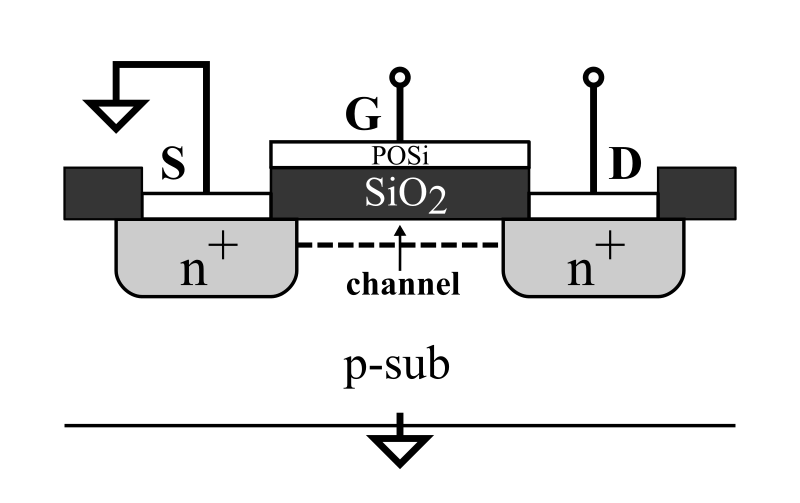
MOSFET(metal-oxide-semiconductor field-effect transister)は上に示すような構造である．
MOSFETにはp型n型の2種類があるが，今回はn型MOSFETで説明する．
MOSは金属と半導体の間に酸化膜がある構造を意味し，ゲート(G)の部分がこの構造となっている．

動作原理

ゲートに電圧をかけていないとき，ドレイン(D)とソース(S)の間はダイオードが背中合わせとなった構造となっているのでドレイン・ソース間に電流は流れない．
ゲートに電圧が加わったとき，酸化膜(${\rm SiO_2}$) が容量となってp型半導体の表面に電子が誘起される．
ゲートに加わる電圧がしきい値電圧$V_{\rm TH}$以上のとき，p型半導体は表面付近のみn型に反転しドレイン・ソース間は(${\rm n^+ n n^+}$)となって電流が流れるようになる．
このn型に反転した領域は，反転領域またはチャネルと呼ばれる．

ピンチオフ現象(MOSFETの電流が飽和する理由)

$V_{\rm D} < V_{\rm G} – V_{\rm TH}$ のとき

$V_{\rm D} < V_{\rm G} – V_{\rm TH}$ のときは$0 \leq x \leq L$ のほとんどの領域で反転層が形成されている．
このときは抵抗と同じように振舞うのでI-V特性は線形になり，$V_{\rm D}$の増加とともに電流も増加する．

$V_{\rm D} > V_{\rm G} – V_{\rm TH}$ のとき

$V_{\rm D}$が$V_{\rm G} – V_{\rm TH}$ を超えてくるとドレイン周辺ではゲートとの間に加わる電圧が減少して，反転層が保てなくなり空乏層となる．
この現象はピンチオフ現象と呼ばれる．
この反転層が保てなくなった地点を次の図に示すように点Pと呼ぶことにする．

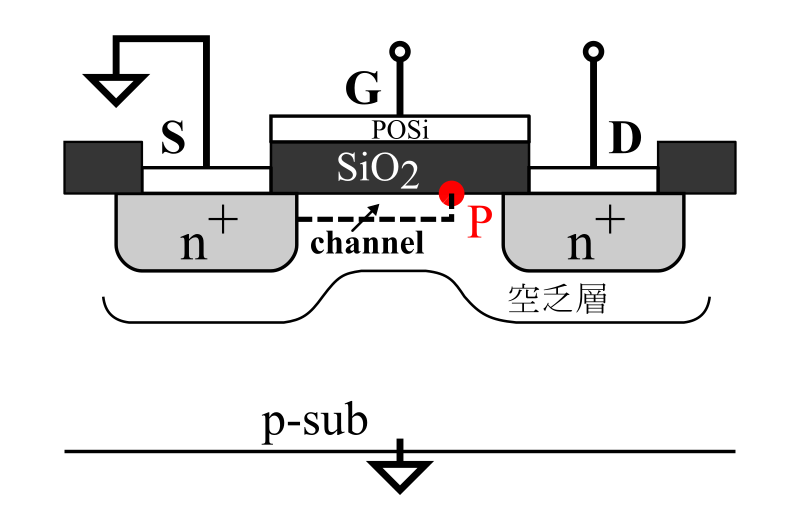
こうなると，$V_{\rm D}$ を上げてもそのほとんどが空乏層にかかるため点Pの電位と位置が大きく変化しなくなる．
後の導出でも使用するが，MOSFETの電流はチャネルにおける$x$方向の電界によってキャリアが加速されて電流が流れるため，点Pの位置と電位が変化しなければ電流値は変化しなくなる，
すなわち飽和するのである．
したがって，MOSFETのI-V特性は次に示すようになる．

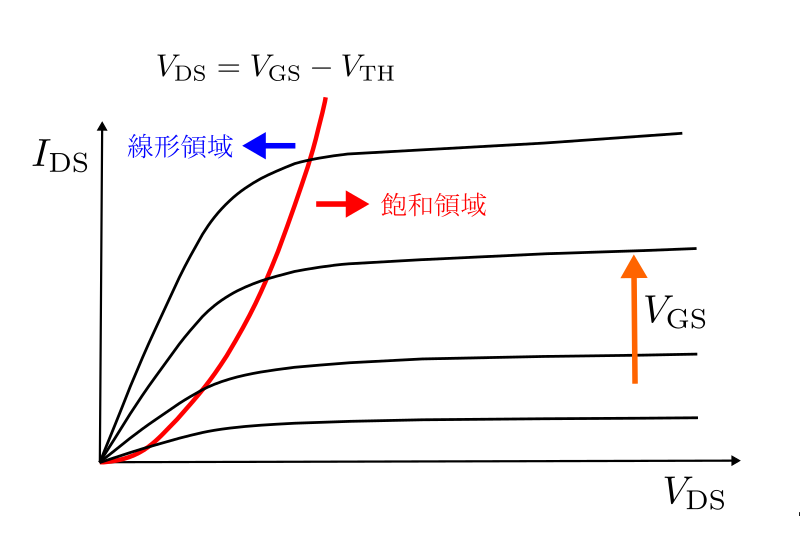
MOSFETの一般的な電流式の導出

次の図に示すように変数及び定数を定義する．

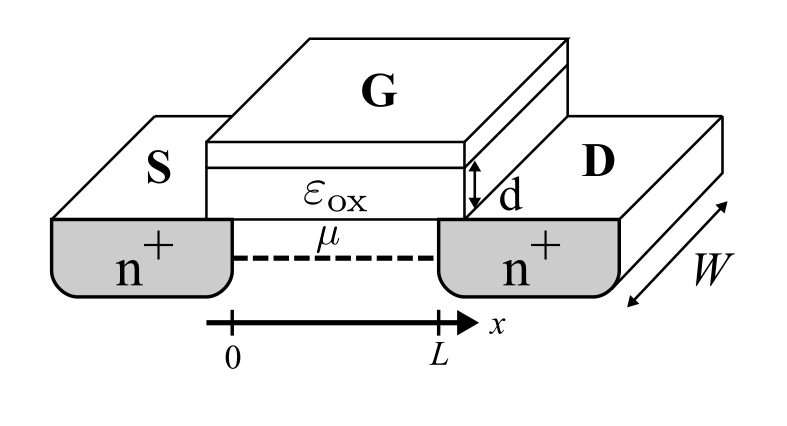
ゲートに正電圧が印加されると絶縁物内に電界が生じて，それによってバルクとなっている半導体の表面に電荷が生じる．
点$x$における単位面積当たりの電荷$Q(x)$は，
$$
Q(x) = C_{\rm ox} \left(V_{\rm G} – V(x) \right) = \frac{\varepsilon_{\rm ox} \varepsilon_{\rm 0}}{d} \left(V_{\rm G} – V(x) \right)
$$
となる．
この誘起された電荷$Q(x)$が$x$方向に生じている電界$dV(x)/dx$によってドレインへと流れていく．
すなわち，この電荷がドリフト電流となって流れるので
$$
\begin{aligned}
I_{\rm D} & = Q(x) \mu \frac{dV(x)}{dx} W \\
& = \frac{\mu \varepsilon_{\rm ox} \varepsilon_0 W}{d} (V_{\rm G} – V(x)) \frac{dV(x)}{dx}
\end{aligned}
$$
ドリフト電流の基本式は$J = Q\mu E$である．
$\mu$ はチャネル内の移動度である．
上式を$0 \sim L$の範囲で$x$で積分すると
$$
\int_0^L I_{\rm D} = \int_0^L \frac{\mu \varepsilon_{\rm ox} \varepsilon_0 W}{d} (V_{\rm G} – V(x)) \frac{dV(x)}{dx} dx
$$
となる．
左辺は任意の$x$で電流が連続なので$I_{\rm D} L$となり，左辺は$x$から$V$への積分に置き換わるので，$V(L) = V_{\rm D}$(ドレイン電圧)を用いて
$$
I_{\rm D} L =\frac{\mu \varepsilon_{\rm ox} \varepsilon_0 W}{d} \int_0^{V_{\rm D}}(V_{\rm G} – V(x)) dV
$$
となる．よって，この式から整理すると
$$
\begin{aligned}
I_{\rm D} &=\frac{\mu \varepsilon_{\rm ox} \varepsilon_0 }{d} \frac{W}{L} \int_0^{V_{\rm D}}(V_{\rm G} – V(x)) dV \\
&=\frac{\mu \varepsilon_{\rm ox} \varepsilon_0 }{d} \frac{W}{L} V_{\rm D} (V_{\rm G} – \frac{1}{2} V_{\rm D})\
\end{aligned}
$$
反転層(チャネル)が形成されるためには$V_{\rm G}$がしきい値電圧$V_{\rm TH}$を超えないといけないので，上の式を$V_{\rm G} \rightarrow V_{\rm G} – V_{\rm TH}$に置き換えて
$$
I_{\rm D} = \frac{\mu \varepsilon_{\rm ox} \varepsilon_0 }{d} \frac{W}{L} V_{\rm D} (V_{\rm G} – V_{\rm TH} – \frac{1}{2} V_{\rm D})
\label{eq:MOScurrent}
$$
と求めることができる．
これがMOSFETで良く知られている電流式である．
この式は$V_{\rm D} < V_{\rm G} – V_{\rm TH}$ のときである線形領域で成り立つ．

ピンチオフ現象と電流飽和

原理の説明で述べた通り，ピンチオフ現象によってMOSFETの電流は飽和する．
飽和するということは傾きが0になるということなので
$$
\frac{\partial I_{\rm D}}{\partial V_{\rm D}} = 0
$$
となるドレイン電圧を求めればよい．
このときのドレイン電圧はピンチオフ電圧と呼ばれ，$V_{\rm DP}$ で表すとする．
上の計算からピンチオフ電圧は
$$
V_{\rm DP} = V_{\rm G} – V_{\rm TH}
$$
と求められる．
ピンチオフ電圧を\eqref{eq:MOScurrent}に代入すると，飽和したときの電流値を求めることができて
$$
I_{\rm D} = \frac{\mu \varepsilon_{\rm ox} \varepsilon_0 }{d} \frac{W}{L} \frac{(V_{\rm G} – V_{\rm TH})^2}{2}
$$
となる．
この式は，二乗則と呼ばれる．

空乏層容量を考慮した場合

空乏層容量$C_{\rm D}$を考慮すると，ゲートに印加した電圧が全て酸化膜にかかるわけではない．
酸化膜容量$C_{\rm OX}$と空乏層容量$C_{\rm D}$の間に
$$
\frac{C_{\rm D}}{C_{\rm OX}} = n-1
$$
が成り立っているとすると，上で示した二乗則の電流式は
$$
I_{\rm D} = \frac{\mu \varepsilon_{\rm ox} \varepsilon_0 }{nd} \frac{W}{L} \frac{(V_{\rm G} – V_{\rm TH})^2}{2}
$$
と表される．
より簡単に表すために$W/L$と$(V_{\rm G}-V_{\rm TH})^2$ を除く文字をまとめて$K’_n$で表す．すなわち，
$$
K’_n = \frac{\mu \varepsilon_{\rm ox} \varepsilon_0 }{2nd}
$$
とすると，ドレイン電流は
$$
I_{\rm D} = K’_n \frac{W}{L} (V_{\rm G} – V_{\rm TH})^2
$$
と表すことができる．

まとめ

MOSFETの電流式は線形領域では，
$$
I_{\rm D} = \frac{\mu \varepsilon_{\rm ox} \varepsilon_0 }{d} \frac{W}{L} V_{\rm D} (V_{\rm G} – V_{\rm TH} – \frac{1}{2} V_{\rm D})
$$
となる，一方，飽和領域では
$$
I_{\rm D} = \frac{\mu \varepsilon_{\rm ox} \varepsilon_0 }{d} \frac{W}{L} \frac{(V_{\rm G} – V_{\rm TH})^2}{2}
$$
となり，二乗則として知られている．