ソース接地回路に抵抗を付した場合の特性について.
ソース抵抗
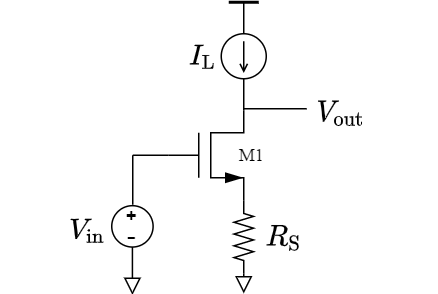
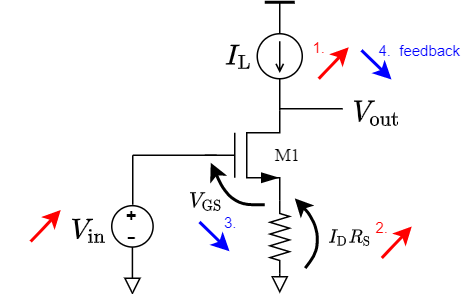
次に示すように,抵抗を介してソースが接地されている増幅器を考える.
この抵抗はソース抵抗やdegeneration抵抗と呼ばれる.
定性的な動作の説明
まず,図の回路の動作を定性的に説明する.
$V_{\rm in}$ が増加したときを考えると以下の過程でフィードバックがかかる.
- ドレイン電流$I_{\rm D}$ が増える
- ソース抵抗 $R_{\rm S}$ の端子電圧$R_{\rm S} I_{\rm D}$ が増加,すなわち$V_{\rm GS}$ が減少
- ゲート・ソース間電圧$V_{\rm GS}$ が減少
- ドレイン電流$I_{\rm D}$ が減る
このフィードバックによって,入力電圧$V_{\rm in}$に対するドレイン電流の変化が小さくなる.
よって得られるゲインは小さくなるが,線形性が高いことが特徴である(後述)
ソース抵抗を挿入した際の相互コンダクタンス
ソース抵抗を含めた回路部分を1つの回路ブロックとして見て,等価等価コンダクタンス$G_{\rm m}$ を考える.
等価相互コンダクタンスの定義は
$$
G_{\rm m} = \frac{\partial I_{\rm D}}{\partial V_{\rm in}}
$$
で表せる.また,上記の回路においては
$$
G_{\rm m} = \frac{\partial I_{\rm D}}{\partial V_{\rm in}} = \frac{\partial I_{\rm D}}{\partial V_{\rm GS}} \frac{\partial V_{\rm GS}}{\partial V_{\rm in}} = g_{\rm m} \frac{\partial V_{\rm GS}}{\partial V_{\rm in}}
$$
となる.また,ゲート・ソース間電圧は
$$
V_{\rm GS} = V_{\rm in} – I_{\rm D} R_{\rm S}
$$
なので,両辺 $V_{\rm in}$ で偏微分すると
$$
\frac{\partial V_{\rm GS}}{\partial V_{\rm in}} = 1 – R_{\rm S} \frac{\partial I_{\rm D}}{\partial V_{\rm in}} = 1 – R_{\rm S} G_{\rm m}
$$
となる.これを $G_{\rm m}$ の式に代入することで次のように求められる.
$$
\begin{aligned}
G_{\rm m} &= g_{\rm m} (1 – R_{\rm S} G_{\rm m}) \nonumber \\
(1 + R_{\rm S} g_{\rm m}) G_{\rm m} &= g_{\rm m} \nonumber \\
G_{\rm m} &= \frac{g_{\rm m}}{(1 + R_{\rm S} g_{\rm m})}
\end{aligned}
$$
このように,ソース抵抗を挿入することによって回路全体のゲインが挿入前よりも小さくなる.
これが由来でソース抵抗はdegeneration抵抗とも呼ばれる(degeneration:退化).
$R_{\rm S} \gg 1/g_{\rm m}$ のときは
$$
G_{\rm m} = \frac{\partial I_{\rm D}}{\partial V_{\rm in}} \simeq \frac{1}{R_{\rm S}}
$$
となるので,入力電圧に対するドレイン電流特性の線形性が高いことになる.
ただし,前述したとおりゲインが小さいのと,ソース抵抗のノイズが大きい欠点がある.
まとめ
ソース接地回路のソースに抵抗を挿入することで,線形性が高くなることが期待できるが,ゲインが小さくなりまたノイズも増加する.
この抵抗は単にソース抵抗やdegeneration抵抗と呼ばれる.
参考文献
[1] Willy, Sansen. Analog Design Essentials. Springer Science & Business Media, 2007, chapter #2
[2] Behzad Razavi(2003),「アナログCMOS集積回路の設計」,丸善出版,pp.73-82.