この記事ではインバータ(inverter)の特性としきい値電圧の導出を行う.
ディジタル回路でいうNOTゲートである.
インバータの特性
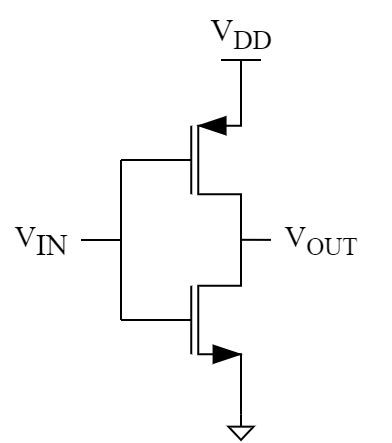
インバータは次のようにp型とn型MOSFETを1つずつ用いた回路である.
ディジタル回路的には,入力HIGH⇒出力LOW,入力LOW⇒出力HIGHとなる回路である.
より詳しく見ると次の図に示すような入出力特性となり,入力電圧によってMOSFETの動作領域は表に示すように5つに分けられる.
次に,インバータの出力が切り替わるしきい値電圧について述べる.
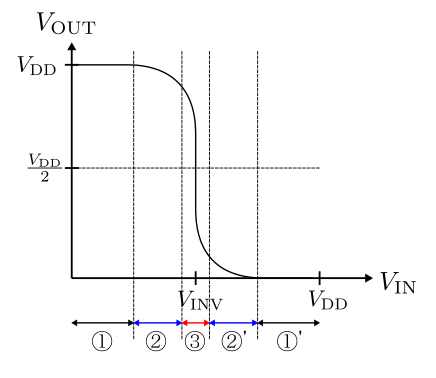
| 入力範囲 | p型 | n型 | 出力 |
|---|---|---|---|
| ① | 飽和領域 | OFF | HIGH |
| ①’ | OFF | 飽和領域 | LOW |
| ② | 飽和領域 | 線形領域 | HIGH |
| ②’ | 線形領域 | 飽和領域 | LOW |
| ③ | 飽和領域 | 飽和領域 | 不安定 |
インバータのしきい値電圧
インバータにしきい値電圧付近の入力電圧が与えられているときは,多くの場合p型とn型MOSFETは共に飽和領域で動作すると考えられるので,飽和領域で動作していることを前提として導出を行う.
電源電圧が著しく低い場合などは当てはまらないことに注意である.
インバータのしきい値電圧の導出
p型MOSFETとn型MOSFETの飽和領域での電流式はそれぞれ
$$
I_{\rm p} = \beta_{\rm p} (V_{\rm GS} – V_{\rm THP})^2, \;
I_{\rm n} = \beta_{\rm n} (V_{\rm GS} – V_{\rm THN})^2
$$
で表される.
$\beta_{\rm p}, \beta_{\rm n}$ は定数で詳しくは後述する.
これを電源電圧$V_{\rm DD}$のインバータに当てはめるとn型の電流は
$$
I_{\rm n} = \beta_{\rm n} (V_{\rm IN} – V_{\rm THN})^2
$$
となる.一方,p型MOSFETの場合は$V_{\rm THP} < 0$ に注意して
$$
I_{\rm p} = \beta_{\rm p} (V_{\rm IN} – V_{\rm DD} + V_{\rm THP})^2 = \beta_{\rm p} (V_{\rm DD} – V_{\rm IN} – |V_{\rm THP}|)^2
$$
これらが等しくなるときの$V_{\rm IN}$ を求めると,
$$
\begin{aligned}
\beta_{\rm n} (V_{\rm IN} – V_{\rm THN})^2 & =
\beta_{\rm p} (V_{\rm DD} – V_{\rm IN} – |V_{\rm THP}|)^2 \\
(V_{\rm IN} – V_{\rm THN}) \sqrt{\frac{\beta_{\rm n}}{\beta_{\rm p}}} & = V_{\rm DD} – V_{\rm IN} – |V_{\rm THP}| \\
\left(1 + \sqrt{\frac{\beta_{\rm n}}{\beta_{\rm p}}} \right) V_{\rm IN} & = V_{\rm DD} – |V_{\rm THP}| + \sqrt{\frac{\beta_{\rm n}}{\beta_{\rm p}}} V_{\rm THN} \\
V_{\rm IN} & = \frac{V_{\rm DD} – |V_{\rm THP}| + \sqrt{\frac{\beta_{\rm n}}{\beta_{\rm p}}} V_{\rm THN}}{1 + \sqrt{\frac{\beta_{\rm n}}{\beta_{\rm p}}}} \\
\end{aligned}
$$
となる.したがって,インバータのしきい値電圧$V_{\rm INV}$は
$$
V_{\rm INV} = \frac{V_{\rm DD} – |V_{\rm THP}| + \sqrt{\frac{\beta_{\rm n}}{\beta_{\rm p}}} V_{\rm THN}}{1 + \sqrt{\frac{\beta_{\rm n}}{\beta_{\rm p}}}}
$$
と求められる.
p型とn型のしきい値が同じ($V_{\rm THP} = V_{\rm THN})$ かつ $\beta_{\rm p} = \beta_{\rm n}$ のときは,
$$
V_{\rm INV} = \frac{1}{2} V_{\rm DD}
$$
と直観と合う結果となるが,かなり理想的な状態である.
しきい値電圧が$V_{\rm DD}/2$からずれる理由
しきい値電圧が$V_{\rm INV} = V_{\rm DD}/2$になるのはかなり理想的な状況と言ったが,実際はどうなのかについて述べる.
MOSFETの電流式で登場した$\beta_{\rm n}, \beta_{\rm p}$は
$$
\beta_{\rm n} = \frac{\mu_{\rm n} \varepsilon_{\rm ox} \varepsilon_0 }{d} \frac{W_{\rm n}}{L_{\rm n}}, \; \beta_{\rm p} = \frac{\mu_{\rm p} \varepsilon_{\rm ox} \varepsilon_0 }{d} \frac{W_{\rm p}}{L_{\rm p}}
$$
と表される.
$L, W$はそれぞれゲート長とゲート幅,$\varepsilon_{\rm OX}, d$はそれぞれ酸化膜の比誘電率と厚さを表している.
$\mu_{\rm n}, \mu_{\rm p}$はそれぞれ電子と正孔の移動度である.
また簡単のため,今後 $W/L$ のことをアスペクト比と呼ぶ.
移動度はキャリアによって違い, $\mu_{\rm n} = (2 \sim 3) \mu_{\rm p}$ であり,同じアスペクト比の場合一般的にn型の方が駆動力が高い.
よって,n型とp型のアスペクト比が等しいときは $\beta_{\rm n} = (2 \sim 3)\beta_{\rm p}$ となり,しきい値電圧は小さくなる.
そういう事情で,一般的にはp型のアスペクト比をn型のアスペクト比の$2 \sim 3$倍に設定される.
すなわち,キャリアの移動度による違いを,アスペクト比すなわちサイジングによって調整することで,結果的に $\beta_{\rm p} \simeq \beta_{\rm n}$ にできる.
これで,しきい値電圧は $V_{\rm DD}/2$ に近づけることができる.
しかし,結局はMOSFETの製造時のばらつきによっても左右されるのでぴったり合うことはないし,実用上合わせる必要もあまりない.
まとめ
インバータはディジタル回路で最も基本的な回路で,入力HIGH⇒出力LOW,入力LOW⇒出力HIGHとなる.
インバータのしきい値電圧は
$$
V_{\rm INV} = \frac{V_{\rm DD} – |V_{\rm THP}| + \sqrt{\frac{\beta_{\rm n}}{\beta_{\rm p}}} V_{\rm THN}}{1 + \sqrt{\frac{\beta_{\rm n}}{\beta_{\rm p}}}}
$$
となる.
ディジタル回路ではしきい値電圧に近い入力電圧を与える時間,すなわち遷移時間を短くした方が消費電力的に有利になる.
また,ゲインが取りにくい集積回路では動作点がしきい値電圧のアンプとしても用いられることがある.