この記事ではソース接地回路の周波数特性について述べる.
主に,周波数特性やバンド幅がどう決まるのかについて.
ソース接地回路
ソース接地回路とは次に示すようにソースが接地された増幅回路である.
図は電流源を負荷としたソース接地回路である.
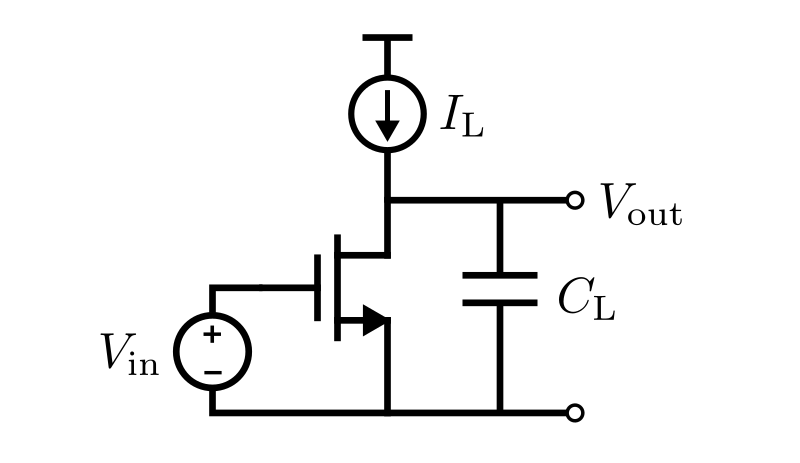
ソース接地回路の基礎的な事項は次の記事を参照.
ソース接地回路の周波数特性
先ほどの回路を小信号等価回路に置き換えると次のようになる.
$r_{\rm ds}$ はドレインソース間抵抗である.
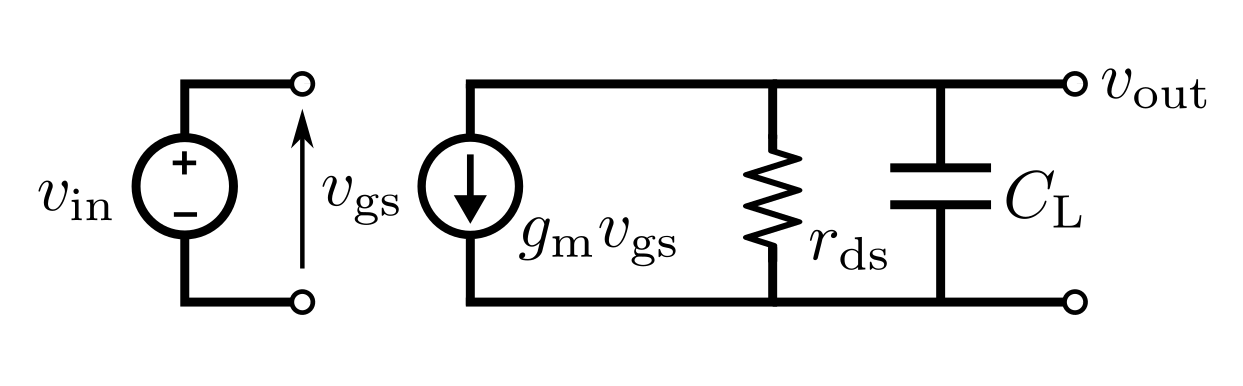
$r_{\rm ds}$と$C_{\rm L}$ の並列回路に$g_{\rm m} r_{\rm ds}$が流れるので,
$$ v_{\rm out} = -\frac{g_{\rm m}}{r_{\rm ds}//(1/ j\omega C_{\rm L})} v_{\rm gs} = – \frac{g_{\rm m} r_{\rm ds} }{1 + j\omega C_{\rm L} r_{\rm ds}} v_{\rm gs} $$
ただし,上の式では並列接続のインピーダンスを//で表している.したがって,電圧利得$A_{\rm v}$ は
$$ A_{\rm v} = -\frac{g_{\rm m} r_{\rm ds} }{1 + j\omega C_{\rm L} r_{\rm ds}} $$
と求まる.この式は,大まかに
$$ A_{\rm v} = g_{\rm m} r_{\rm ds} (\omega < \frac{1}{C_{\rm L} r_{\rm ds}}) $$ $$\frac{g_{\rm m}}{j\omega C_{\rm L}} (\omega > \frac{1}{C_{\rm L} r_{\rm ds}}) $$
の2曲線を考えて図示すると分かりやすい.
これより,模式的にゲインと位相の周波数特性を描くと次のようになる.
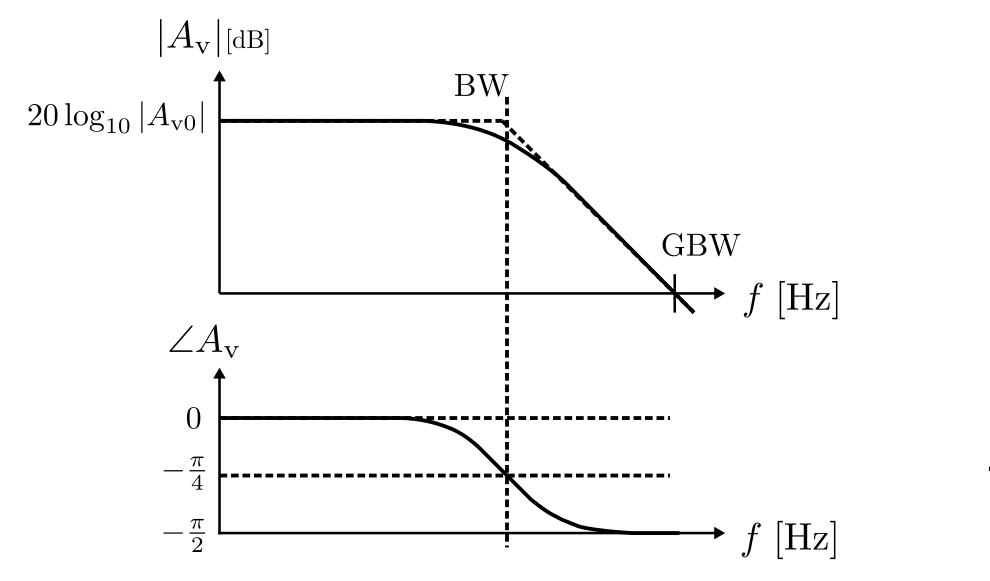
バンド幅 (BW:Band-Width)
バンド幅は低周波成分の電圧増幅率$A_{\rm v0} = g_{\rm m} r_{\rm ds}$ の$1/ \sqrt{2}$ (dBで表すと$-3 {\rm dB} $)より大きいゲインが得られる周波数の幅を指す.
今回の場合は,ハイパスフィルタであるので$0 \sim f_{\rm c}$ の間となる($f_{\rm c}$はカットオフ周波数).
よって,カットオフ周波数を求めると,
$$ \omega_{\rm c} = \frac{1}{r_{\rm ds} C_{\rm L} }, ~~f_{\rm c} = \frac{1}{2\pi r_{\rm ds} C_{\rm L} } $$
バンド幅BWは,$0 \sim f_{\rm c}$の幅なのでそのまま
$$ {\rm BW} = \frac{1}{2 \pi r_{\rm ds} C_{\rm L} } $$
となる.
GB積 (GBW:Gain-Band-Width-product)
GB積とは電圧増幅率$A_{\rm v0}$ とバンド幅BWの積で
$$ {\rm GBW} = A_{\rm v0} \cdot \rm{BW} $$
である.次の図のように,$\omega < 1/r_{\rm ds} g_{\rm m}$ の領域であれば,$GBW = A_{\rm v} f$ が成立する.
これより,$\omega < 1/r_{\rm ds} g_{\rm m}$ の周波数ではどのぐらいのゲインが得られるかをGBWが分かるだけで見積もることができる.
また,${\rm GBW} = A_{\rm v} f$ が成立することから$A_{\rm v} = 1 $となる点(ボード線図で言うとx切片)からGBWを読み取ることができる.
ソース接地回路のGBW
1段の場合は,
$$ {\rm GBW} = g_{\rm m} r_{\rm ds} \cdot \frac{1}{2 \pi r_{\rm ds} C_{\rm L}} = \frac{g_{\rm m}}{2 \pi C_{\rm L} } $$
となる.
GBWは出力抵抗$r_{\rm ds}$ に依存せず,相互インダクタンス$g_{\rm m}$ と負荷容量$C_{\rm L}$にのみ依存する.
負荷を接続しない場合
基本的に負荷を接続して使用するので上の場合だけで十分だが,負荷を接続しない場合はどの成分によって周波数特性が決まるのか見ておく.
次の図のように負荷を接続しないまたは小さい場合は,ゲートにおける配線などの入力抵抗$R_{\rm S}$ と$C_{\rm gs}$ によって決まる.
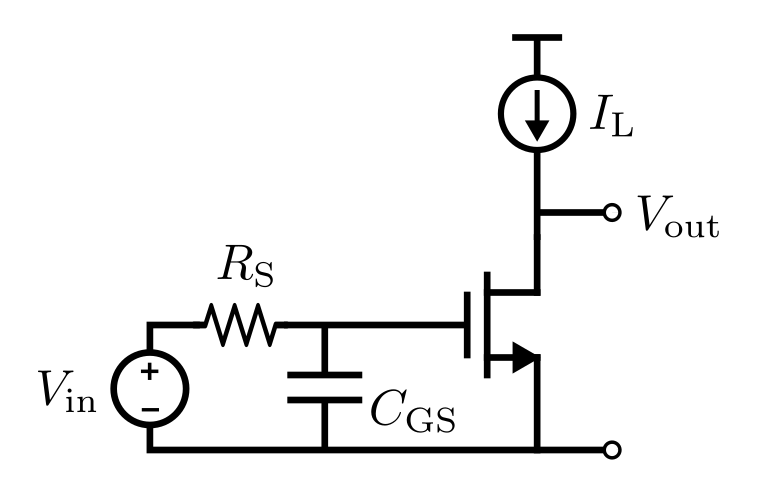
周波数特性の概形は負荷容量があった時と同じであるが,バンド幅は,
$$ {\rm BW} = \frac{1}{2 \pi R_{\rm S} C_{\rm gs} } $$
となる.
低周波のときの増幅率$A_{\rm v0}$ は$A_{\rm v0} = g_{\rm m} r_{\rm ds}$ なので,GB積は,
$$ {\rm GBW} = A_{\rm v0} \cdot \rm{BW} = \frac{g_{\rm m}}{2 \pi C_{\rm gs}} \frac{r_{\rm ds}}{R_{\rm S}} = f_{\rm T} \frac{r_{\rm ds}}{R_{\rm S}} $$
となる.
$f_{\rm T} = g_{\rm m} / 2 \pi C_{\rm gs}$ はトランジット周波数で,MOSFETのサイズや動作点で変わるパラメータである.
簡単に言えば,MOSFETが動作可能な最高周波数である.
まとめ
ソース接地回路について1段の場合
$$ A_{\rm v0} = g_{\rm m} r_{\rm ds} $$
$$ {\rm BW} = \frac{1}{2 \pi r_{\rm ds} C_{\rm L} } $$
$$ {\rm GBW} = \frac{g_{\rm m} }{2 \pi C_{\rm L} } $$
が成り立つ.
この関係はアンプの設計などの際は電圧増幅率から$g_{\rm m}$ を介して,MOSFETのバイアス電圧の決定などに使用する重要な関係にとなる.
参考文献
[1] Willy, Sansen. Analog Design Essentials. Springer Science & Business Media, 2007, chapter #2
[2] Behzad Razavi(2003),「アナログCMOS集積回路の設計」,丸善出版.
[3] LSI設計者のためのCMOSアナログ回路入門(2017),「LSI設計者のためのCMOSアナログ回路入門」,CQ出版社.


kenzoさん。
貴重な情報の発信ありがとうございます。
一点可能であれば教えていただきたいのですが、こちらのサイトで取り上げられているソース接地回路の小信号等価回路にC_Lが並立に挿入されているのはなぜなのでしょうか?
学校では、小信号等価回路はキャパシタはショート扱いでよいと教わったので、よくわからないのです。
お読みいただき誠にありがとうございます.返答が遅れすいません.
ソース接地回路は電圧増幅などのバッファ回路として使用され,出力(図での出力Vout)にMOSFETのゲート(次の回路の入力端子)が接続されることが多いです.
このような場合,出力Voutに接続されているゲート容量が見えることになりますので,出力には次段の負荷容量CLが接続されているとして,考えることが多いです.
※おっしゃられている「キャパシタをショート扱い」というのは,かなり高周波での話だと思われ,インピーダンス(1/jwC)がかなり小さい場合のみだと思います.