カレントミラー回路の原理と精度

この記事では頻繁に使用するカレントミラー回路(current mirror)について原理を説明する．
また，電流のコピー精度についても触れる．

カレントミラー回路
原理
カレントミラーの誤差原因
1. しきい値電圧の違い
2. 飽和領域の$I_{\rm DS}-V_{\rm DS}$特性がフラットでない
まとめ
参考文献

カレントミラー回路

カレントミラー回路は次に示すような回路で，簡単に言うと参照電流源$I_{\rm in}$を$I_{\rm out}$に$B$倍にコピーする回路である．

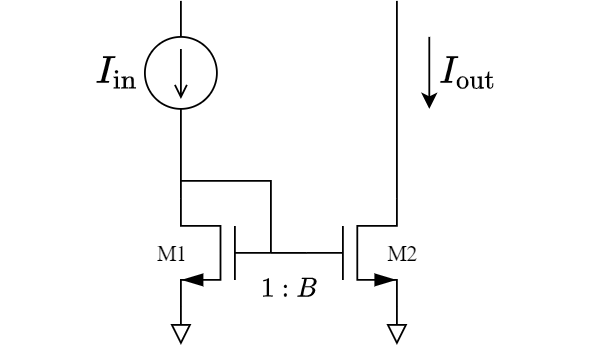
原理

MOSFETの飽和領域での電流式は，
$$
I_{\rm D} = \beta (V_{\rm G} – V_{\rm TH})^2
$$
と表せる(二乗則)．
より詳しくは以下を参照して頂きたい．

カレントミラー回路ではM1とM2のゲート電圧は同じであるため，これを$V_{\rm G}$と置く．
図のM1とM2に二乗則を適用すると
$$
\begin{aligned}
I_{\rm in} &= \beta_{\rm 1} (V_{\rm G} – V_{\rm TH1})^2 \\
I_{\rm out} &= \beta_{\rm 2} (V_{\rm G} – V_{\rm TH2})^2
\end{aligned}
$$
と表せる．
簡単のために，2つのMOSFETのしきい値電圧は同じ ($V_{\rm TH1} = V_{\rm TH2}$)とすると，$I_{\rm out} / I_{\rm in}$ は，
$$
\frac{I_{\rm out}}{I_{\rm in}} = \frac{\beta_{\rm 2}}{\beta_{\rm 1}}
$$
となる．
よって，$\beta_{\rm 2}/\beta_{\rm 1} = 1$ とすれば電流をコピーできることになる．
もちろん，$\beta_{\rm 2}/\beta_{\rm 1} = B$ などとすれば入力電流の定数倍の電流値を設定することもできる．

カレントミラーの誤差原因

カレントミラーの誤差の原因は様々考えられるが，今回は以下の2つを挙げる．

2つのMOSFETのしきい値電圧の違い
飽和領域の$I_{\rm DS}-V_{\rm DS}$特性が完全にフラットではない

しきい値電圧の違い

2つのMOSFETのしきい値電圧が違うことで，原理の説明で行った計算の途中からは理想的に成立しなくなる
この結果，出力電流が予想値とずれ得る．
防止策として，しきい値電圧のばらつきはMOSFETの面積が大きい方が小さいので，サイズの大きいMOSFETが使われる．

飽和領域の$I_{\rm DS}-V_{\rm DS}$特性がフラットでない

MOSFETの飽和領域の$I_{\rm DS}-V_{\rm DS}$特性は次の図に示すように完全にフラットではなく，$V_{\rm DS}$の増加に伴って電流は増加していく．
バイポーラトランジスタでいうとアーリー効果と同様の現象である．
そもそも，原理の説明で用いた二乗則は電流値が飽和することを前提としているためずれが生じてしまうのである．

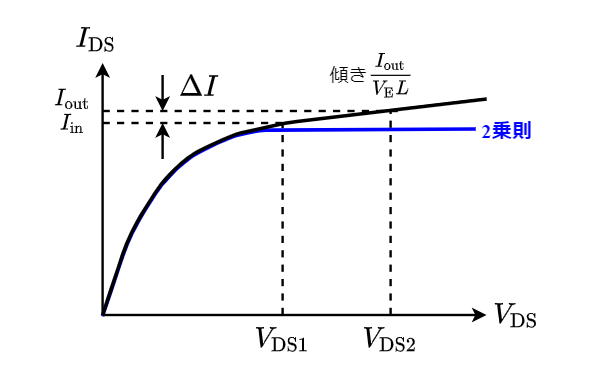
もう少し定量的に評価すると，アーリー電圧が$V_{\rm E} L$ とするならば，$V_{\rm E} L << V_{\rm DS1}, V_{\rm DS2}$とすると
$$
\frac{\Delta I_{\rm DS}}{I_{\rm out}} = \frac{V_{\rm DS2} – V_{\rm DS1}}{V_{\rm E} L}
$$
となる．
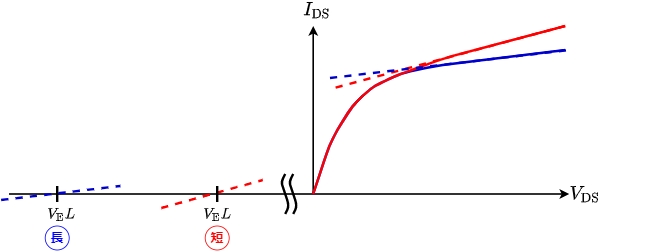
ゲート長$L$が長くなると$I_{\rm DS}-V_{\rm DS}$特性がフラットに近づくために誤差が小さくなるのである．