前回の記事では,伝送線路に電圧を加えるとき,すなわち伝送線路での送端での現象について解説した.
今回の記事では,伝送線路を伝わって端まで到達したとき,すなわち終端で電圧と電流がどうなるかについて説明していく.
終端における反射
次のように伝送線路の終端に負荷抵抗$R_L$が接続されている場合を考えよう.
今回は,入射波と反射波を考える必要があるので,入射波を添え字i,反射波を添え字rで表す.
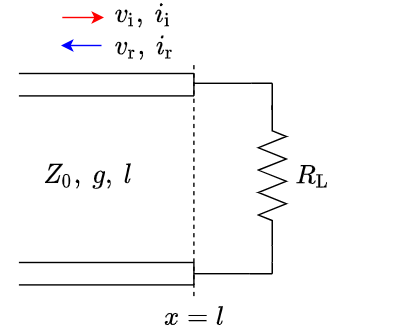
図中の定数
- $Z_0$:伝送線路の特性インピーダンス
- $g$:伝送線路の伝搬速度
- $l$:伝送線路の長さ
- $R_{\rm L}$:出力インピーダンス(LはLoadの頭文字)
- $v_{\rm i}$:電圧の入射波
- $v_{\rm r}$:電圧の反射波
- $i_{\rm i}$:電流の入射波
- $i_{\rm r}$:電流の反射波
前回の記事のように,線路に入った入射波が線路の終端にまで到達したとき,終端抵抗である$R_{\rm L}$の大きさに応じて反射波が発生する.
次からは,$R_{\rm L}$の大きさによって反射波の大きさがどう変わるのかを見ていこう.
電圧反射係数と電流反射係数
伝送線路の終端($x=l$)での境界条件は
$$
v_{\rm i} = Z_0 i_{\rm i}, ~ v_{\rm r} = -Z_0 i_{\rm r}
$$
負荷抵抗$R_{\rm L}$には$x=l$における電流( $i_{\rm i} + i_{\rm r}$ )と電圧( $v_{\rm i} + v_{\rm r}$ )が印加されるので,
$$
v_{\rm i} + v_{\rm r} = R_{\rm L} (i_{\rm i} + i_{\rm r})
$$
となる.これらの条件から式変形をしていくと.
$$
\begin{aligned}
v_{\rm i} + v_{\rm r} &= R_{\rm L} (i_{\rm i} + i_{\rm r}) \\
v_{\rm i} + v_{\rm r} &= R_{\rm L} \left( \frac{v_{\rm i}}{Z_0} – \frac{v_{\rm r}}{Z_0} \right) \\
\left( \frac{R_{\rm L}}{Z_0} + 1 \right) v_{\rm r} &= \left( \frac{R_{\rm L}}{Z_0} – 1 \right) v_{\rm i} \\
v_{\rm r} &= \frac{R_{\rm L} – Z_0}{R_{\rm L} + Z_0} v_{\rm i} \\ &= \gamma_v v_{\rm i} \\
\end{aligned}
$$
というように,入射波と反射波の関係が求められる.
この入射波と反射波の比$\gamma_v$は電圧反射係数と呼ばれ,
$$
\gamma_v = \frac{R_{\rm L} – Z_0}{R_{\rm L} + Z_0}
\label{eq:gamma_v}
$$
となる.
電流にも入射波と反射波の関係を求めることができ,
$$
\begin{aligned}
i_{\rm r} &= – \frac{v_{\rm r}}{Z_0} \\
&= – \frac{R_{\rm L} – Z_0}{R_{\rm L} + Z_0} \frac{v_{\rm i}}{Z_0} \\
&= – \frac{R_{\rm L} – Z_0}{R_{\rm L} + Z_0} i_{\rm i} \\
&= \gamma_i i_{\rm i}
\end{aligned}
$$
の関係が導びかれる.
この入射波と反射波の比$\gamma_i$は電流反射係数と呼ばれ,
$$
\gamma_i = – \frac{R_{\rm L} – Z_0}{R_{\rm L} + Z_0} = -\gamma_v
\label{eq:gamma_i}
$$
となる.
また,電流反射係数が電圧反射係数の$-1$倍になることは覚えておくと便利である.
このように,伝送線路の終端では電圧と電流の反射が起こり,それは伝送線路の特性インピーダンス$Z_0$と終端抵抗$R_{\rm L}$(インピーダンス)によって決まる.
入力波がステップ状のとき
具体例として$R_{\rm L} = 2Z_0$のとき,大きさ$E_0$のステップ状の波が入力された場合を考えよう.
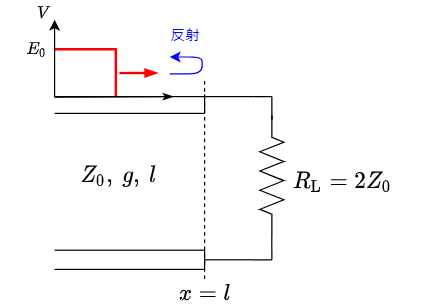
電圧反射係数$\gamma_v$は式\eqref{eq:gamma_v}より,
$$
\gamma_v = \frac{2Z_0 – Z_0}{2Z_0 + Z_0} = \frac{1}{3}
$$
また,電流反射係数$\gamma_i$は
$$ \gamma_i = -\frac{1}{3} $$
と計算できる.
これは次の図のように入射波に対して反射波が発生することになる.
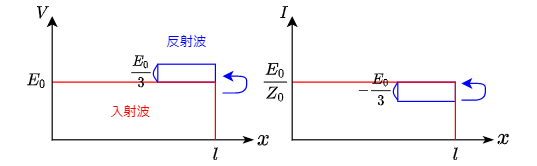
特別な3つの終端パターン
次に,特別な終端パターンとして次の3パターンを考える.
- 開放:$R_{\rm L} = \infty$
- 短絡:$R_{\rm L} = 0$
- 整合:$R_{\rm L} = Z_0$
終端開放 $R_{\rm L} = \infty$
終端が開放の場合は$R_{\rm L} \rightarrow \infty$を考えればよい.
電圧反射係数$\gamma_v$は式\eqref{eq:gamma_v}より,
$$
\gamma_v = \lim_{R_{\rm L} \rightarrow \infty}\frac{R_{\rm L} – Z_0}{R_{\rm L} + Z_0} = 1
$$
と求められる.
よって,電流反射係数は$\gamma_i = -1$となる.
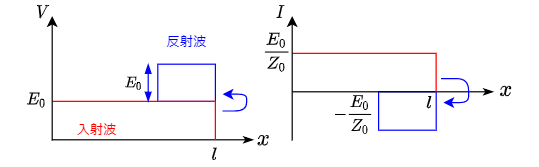
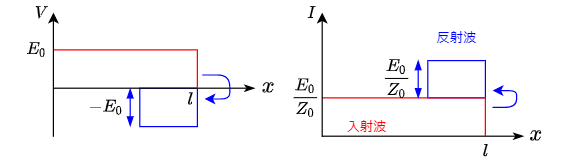
終端短絡 $R_{\rm L} = 0$
終端が短絡の場合は$R_{\rm L} = 0$である.
よって,電圧反射係数は$\gamma_v = -1$,電流反射係数は$\gamma_i = 1$となる.
終端整合 $R_{\rm L} = Z_0$
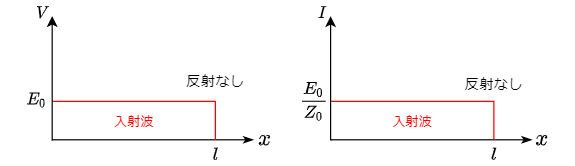
$R_{\rm L} = Z_0$のとき,終端が整合されていると表現される.
このときの電圧反射係数および電流反射係数は共に$\gamma_v = 0$,電流反射係数は$\gamma_i = 0$となる.
すなわち,整合されているときは反射波が発生しないことを表す.
終端が整合されていると色々嬉しいことがあるのだが,具体的には次回に説明する.
まとめ
伝送線路の終端では入射波の反射が起こり,それは伝送線路の特性インピーダンス$Z_0$と終端抵抗$R_{\rm L}$(インピーダンス)によって決まる.
終端における入射波と反射波の関係は
$$
\begin{aligned}
\gamma_v &= \frac{R_{\rm L} – Z_0}{R_{\rm L} + Z_0} ~(電圧反射係数)\\
\gamma_i &= – \frac{R_{\rm L} – Z_0}{R_{\rm L} + Z_0} ~(電流反射係数)
\end{aligned}
$$
となる.電圧反射係数$\gamma_v$と電流反射係数$\gamma_i$の間には
$$
\gamma_i = -\gamma_v
$$
の関係がある.
また,終端が開放,短絡,整合のときの反射係数を表にまとめておく.
特に,終端が整合されているときは反射波が発生しない.
| 終端 | 電圧反射係数 | 電流反射係数 |
|---|---|---|
| 開放 | 1 | -1 |
| 短絡 | -1 | 1 |
| 整合 | 0 | 0 |