この記事では,分布定数回路の基礎方程式について説明し,電信方程式の導出を行う.
集中乗数回路と分布定数回路
次のような線路を考えてみよう.
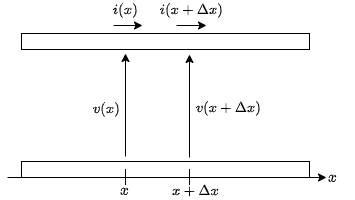
集中定数回路の考え方では,上の線路はどこも同電位かつ同じ電流が流れていると考えるので,
$$
v(x) = v(x+\Delta x), ~i(x) = i(x+\Delta x)
$$
となる.
分布定数回路の考え方では,長距離の配線は抵抗やコンダクタンス,インダクタンス,キャパシタンスが一様に分布していると考える.
これを回路図で考えると次のようになる.
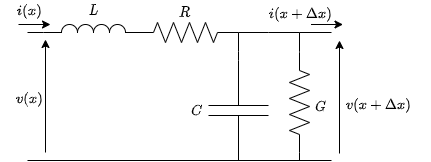
それらの成分によって電圧と電流が変化するのでもちろん,
$$
v(x) \ne v(x+\Delta x), ~i(x) \ne i(x+\Delta x)
$$
となる.
要は,線路は上の回路が無限に繋がったものと捉えることができる.
$R=G=0$として考えることも多く,このときはLCラダーと呼ばれる.
では,線路を上記の回路のように見立てたときに何が言えるのかを見ていく.
分布定数回路の基礎方程式
単位長当たりの抵抗とコンダクタンス,インダクタンスとキャパシタンスをそれぞれ$R[\rm \Omega / m]$,$G[\rm S / m]$,$L[\rm H / m]$,$C[\rm F / m]$ とする.
このとき,KVLとKCLから
\begin{align}
v(x) – v(x + \Delta x) = R \Delta x \cdot i + L \Delta x \frac{\partial i}{\partial t} \\
i(x) – i(x + \Delta x) = G \Delta x \cdot v + C \Delta x \frac{\partial v}{\partial t}
\end{align}
両辺を$\Delta x$ で割ると,
\begin{align}
\frac{v(x) – v(x + \Delta x)}{\Delta x} = R \Delta x \cdot i + L \Delta x \frac{\partial i}{\partial t} \\
\frac{i(x) – i(x + \Delta x)}{\Delta x}= G \Delta x \cdot v + C \Delta x \frac{\partial v}{\partial t}
\end{align}
したがって,$\Delta x \rightarrow 0$ とすると
\begin{align}
\label{eq:basicKVL}
-\frac{\partial v}{\partial x} = R i + L \frac{\partial i}{\partial t} \\
-\frac{\partial i}{\partial x} = G v + C \frac{\partial v}{\partial t}
\label{eq:basicKCL}
\end{align}
の関係が導ける.
これらの式は分布定数回路の基礎方程式と呼ばれる.
電信方程式
基礎方程式は2式であり$i$と$v$を2変数と見るとそれぞれの変数のみの方程式で表すことができる.
以下ではそれぞれ,電圧$v$で表した式と電流$i$のみで表した式の導出を行う.
電圧$v$のみで表した場合
$v$のみであらわしたいので $i$を消去する操作を行っていく.
式\eqref{eq:basicKVL}を両辺$x$で偏微分し,式\eqref{eq:basicKCL}を両辺$t$で偏微分すると
\begin{align}
-\frac{\partial^2 v}{\partial x^2} = R \frac{\partial i}{\partial x} + L \frac{\partial^2 i}{\partial t \partial x} \\
-\frac{\partial^2 i}{\partial x \partial t} = G \frac{\partial v}{\partial t} + C \frac{\partial^2 v}{\partial t^2}
\end{align}
となる.これらの式と,
$$
\frac{\partial^2 v}{\partial x \partial t} = \frac{\partial^2 v}{\partial t \partial x}, ~
-\frac{\partial i}{\partial x} = G v + C \frac{\partial v}{\partial t}
$$
の関係を用いると,
\begin{align}
-\frac{\partial^2 v}{\partial x^2} = -R \left( G v + C \frac{\partial v}{\partial t} \right) – L \left( G \frac{\partial v}{\partial t} + C \frac{\partial^2 v}{\partial t^2} \right) \\
\frac{\partial^2 v}{\partial x^2} = LC \frac{\partial^2 v}{\partial t^2} + \left( CR + LG \right) \frac{\partial v}{\partial t} + RGv
\end{align}
と電流$v$のみを変数とした方程式が導ける.
電流$i$のみで表した場合
同様の手順で$v$を消去する操作を行っていく.
式\eqref{eq:basicKVL}を両辺$t$で偏微分し,式\eqref{eq:basicKCL}を両辺$x$で偏微分すると
\begin{align}
-\frac{\partial^2 v}{\partial x \partial t} = R \frac{\partial i}{\partial t} + L \frac{\partial^2 i}{\partial t^2} \
-\frac{\partial^2 i}{\partial x^2} = G \frac{\partial v}{\partial t} + C \frac{\partial^2 v}{\partial t \partial x}
\end{align}
となる.これらの式と,
$$
\frac{\partial^2 v}{\partial x \partial t} = \frac{\partial^2 v}{\partial t \partial x}, ~
-\frac{\partial v}{\partial x} = R i + L \frac{\partial i}{\partial t}
$$
の関係を用いると,
\begin{align}
-\frac{\partial^2 i}{\partial x^2} = -G \left( R i + L \frac{\partial i}{\partial t} \right) – C \left( R \frac{\partial i}{\partial t} + L \frac{\partial^2 i}{\partial t^2} \right) \\
\frac{\partial^2 i}{\partial x^2} = LC \frac{\partial^2 i}{\partial t^2} + \left( CR + LG \right) \frac{\partial i}{\partial t} + RGi
\end{align}
と電流$i$のみを変数とした方程式が導ける.
まとめ
電信方程式は分布定数回路の基礎方程式から$i$と$v$のみで表すことで導出できる式で
\begin{align}
\frac{\partial^2 i}{\partial x^2} = LC \frac{\partial^2 i}{\partial t^2} + \left( CR + LG \right) \frac{\partial i}{\partial t} + RGi \\
\frac{\partial^2 v}{\partial x^2} = LC \frac{\partial^2 v}{\partial t^2} + \left( CR + LG \right) \frac{\partial v}{\partial t} + RGv
\end{align}
で表される.
特に,$R=G=0$のときは無損失線路と呼ばれ,
$$
\frac{\partial^2 v}{\partial x^2} = LC \frac{\partial^2 v}{\partial t^2} , ~
\frac{\partial^2 i}{\partial x^2} = LC \frac{\partial^2 i}{\partial t^2}
$$
となり,これは波動方程式の形となる.
また,$L=G=0$または$C=R=0$のとき,
$$
\frac{\partial^2 v}{\partial x^2} = GL \frac{\partial^2 v}{\partial t^2} , ~
\frac{\partial^2 i}{\partial x^2} = RC \frac{\partial^2 i}{\partial t^2}
$$
となり,熱伝達の方程式の形となる.