この記事では,電信方程式の物理的意味と導出方法について解説する.
電信方程式は分布定数回路の基礎方程式から導かれる2階の偏微分方程式で,次に示すようなものである.
$$
\begin{aligned}
\frac{\partial^2 i}{\partial x^2} = LC \frac{\partial^2 i}{\partial t^2} + \left( CR + LG \right) \frac{\partial i}{\partial t} + RGi \\
\frac{\partial^2 v}{\partial x^2} = LC \frac{\partial^2 v}{\partial t^2} + \left( CR + LG \right) \frac{\partial v}{\partial t} + RGv
\end{aligned}
$$
この方程式の解を得ることで,電流$i$または電圧$v$がどのように線路を伝わっていくのかが分かる.
今回は,無損失($R=G=0$)の場合に着目してその解を示し物理的意味を説明する.
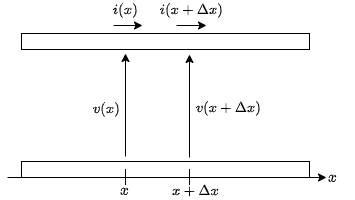
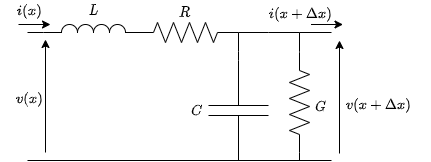
また,気になる方のために次の記事で導出方法を記している.
無損失の場合の電信方程式の解
無損失の場合($R=G=0$)の電信方程式は
$$
\frac{\partial^2 v}{\partial x^2} = LC \frac{\partial^2 v}{\partial t^2} , ~
\frac{\partial^2 i}{\partial x^2} = LC \frac{\partial^2 i}{\partial t^2}
$$
となり,波動方程式の形になるのであった.
分布定数線路は抵抗成分とコンダクタンス成分がないので,以下の線路(LCラダー)を考えていることになる.
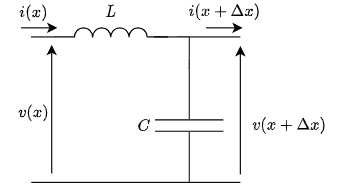
無損失の場合の解
無損失の場合,電信方程式は波動方程式の形となりその解はダランベールの解の形で得られることが知られている.
よって,無損失の場合の電信方程式の解は,
$$
\left( \begin{array}{c} v \\ i \end{array} \right) =
\left(
\begin{array}{c}
f_1 \left(x-\frac{1}{\sqrt{LC}} t \right) + f_2 \left(x + \frac{1}{\sqrt{LC}} t \right) \\
\sqrt{\frac{C}{L}} f_1 \left(x-\frac{1}{\sqrt{LC}} t \right) – \sqrt{\frac{C}{L}} f_2 \left(x + \frac{1}{\sqrt{LC}} t \right)
\end{array}
\right)
$$
となる.
$f_1$と$f_2$は初期条件や境界条件によって決まる関数である.
もう少し簡単に書くと次のようになる.
$$
\left( \begin{array}{c} v \\ i \end{array} \right) =
\left(
\begin{array}{c}
f_1 \left(x-gt \right) + f_2 \left(x + gt \right) \\
\frac{1}{Z} f_1 \left(x-gt \right) – \frac{1}{Z} f_2 \left(x + gt \right)
\end{array}
\right)
$$
上式の$Z$と$g$は,
$$
Z = \sqrt{\dfrac{L}{C}}, ~ g=\dfrac{1}{\sqrt{LC}}
$$
であり,$Z$は特性インピーダンス,$g$は伝搬速度を表す.
解の物理的意味
簡単のために$f_1, ~ f_2$ にはステップ関数として考えよう.
電圧に着目すると,次の図のように x軸の+方向の波(前進波)と x軸の-方向の波(後進波)の重ね合わせで表されていることが分かる.
それらの進む速度が伝搬速度$g$ である.
また,電流に関しても同様のことが言えて,特性インピーダンスはそれぞれの進行波における電圧と電流の振幅比と見れる.
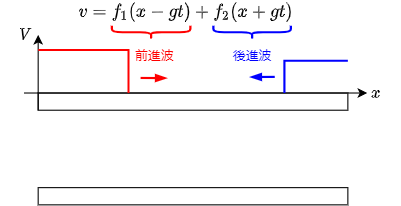
- 補足
$f(x-gt)$ : 前進波
$x-gt=\eta(\rm const.) \Leftrightarrow$ $x = \eta + gt$ より $t$が増加すると$x$が増加
$f(x-gt)$ : 後進波
$x-gt=\xi(\rm const.) \Leftrightarrow$ $x = \xi – gt$ より $t$が増加すると$x$が減少
まとめ
無損失の線路の電信方程式は波動方程式となるのでダランベールの解となり,次のように進行波と後退波の重ね合わせで表される.
$$
\left(
\begin{array}{c}
v \\ i
\end{array}
\right) =
\left(
\begin{array}{c}
f_1 \left(x-gt \right) + f_2 \left(x + gt \right) \\
\frac{1}{Z} f_1 \left(x-gt \right) – \frac{1}{Z} f_2 \left(x + gt \right)
\end{array}
\right)
$$
ただし,$Z$は特性インピーダンス,$g$は伝搬速度を表し,
$$
Z = \sqrt{\dfrac{L}{C}}, ~ g=\dfrac{1}{\sqrt{LC}}
$$
である.