この記事では,伝送線路に電圧を与えたときどのように考えていけば良いかを解説していく.
まず,送信側の電圧源(送端)でどのように電圧及び電流が伝わっていくかを見ていく.
伝送線路に入射するときの振舞い
次のように伝送線路に出力抵抗が$R_S$の電圧源を接続した場合を考えよう.
また,スイッチは初期状態がOFFで$t=0$にONにする.
伝送線路は初期状態での電圧・電流は0のとき,すなわち
$$
v(x, 0) = 0, ~ i(x, 0) = 0
$$
のときを考える.
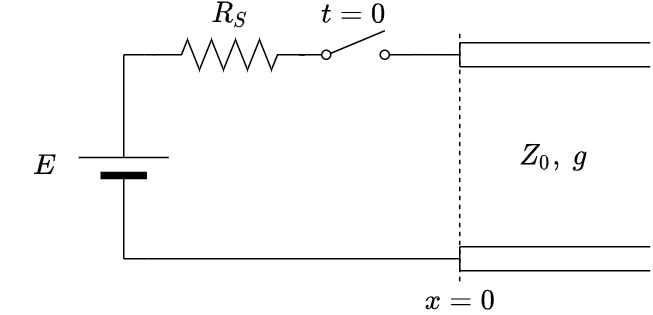
図中の定数
- $Z_0$:伝送線路の特性インピーダンス
- $g$:伝送線路の伝搬速度
- $R_S$:出力インピーダンス(SはSourceの頭文字)
境界条件と送端における振る舞い
ダランベールの解から,伝送線路の電圧分布は任意の関数$f_1, ~f_2$を用いて
$$
v(x, t) = f_1(x-gt) – f_2(x + gt)
$$
であるのであった.
$f_1$は進行波で$f_2$は後退波であるが,スイッチを閉じた直後は反射波はないと考えてよい.
よって,$f_2 = 0$となって
$$
v(x, t) = f_1(x-gt), ~ i(x, t) = \frac{1}{Z_0} f_1(x – gt)
$$
と簡単になる.
このとき,境界$x = 0$において
$$
v(0, t) = Z_0 i(0, t)
$$
の関係が成り立つので,今回の場合はただの抵抗として扱えることになる.
すなわち,次の回路を考えているのと同じになる.
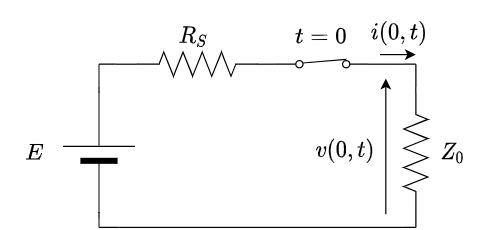
よって,伝送線路の端( $x = 0$ )には
$$
\begin{aligned}
v(0, t) &= f_1(-gt) = \frac{Z_0}{R_S + Z_0} E\cdot H(t) \\
i(0, t) &= \frac{1}{Z_0} f_1(-gt) = \frac{E}{R_S + Z_0} \cdot H(t)
\end{aligned}
$$
の抵抗によって分圧された大きさのステップ状の波が入力されることになる.
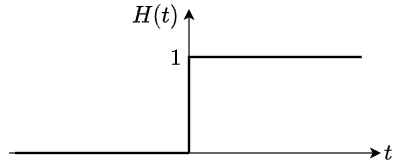
$H(t)$はヘビサイド関数と呼ばれるが,次のようにただのステップ状の関数である.
よって,位置$x$においては
$$
-gt = x – gt’ \Leftrightarrow t’ = t-\frac{x}{g}
$$
と置き直すことによって求めることができて
$$
\begin{aligned}
v(x, t) &= f_1(x-gt) = \frac{Z_0}{R_S + Z_0} E\cdot H(t – \dfrac{x}{g}) \\
i(x, t) &= \frac{1}{Z_0} f_1(x-gt) = \frac{E}{R_S + Z_0} \cdot H(t – \dfrac{x}{g})
\end{aligned}
$$
と求めることができる.
これは次に示すようにスイッチを閉じた直後,速度$g$で分圧電圧が伝わるということになる.
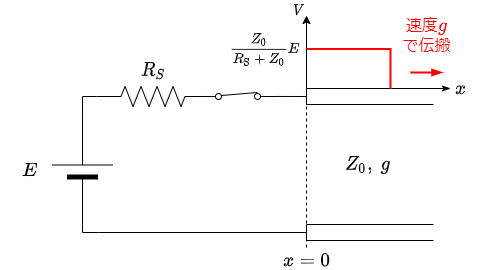
まとめ
伝送線路にステップ状の電圧を印加する場合を例に挙げて伝送線路の送端における現象について述べた.
この記事の条件では,伝送線路は抵抗$Z_0$の抵抗として考え,印加した電圧の分圧$Z_0/(R_S + Z_0)E$の電圧が線路に入っていく.