この記事では,無損失の場合について電信方程式の解の導出方法について解説する.
無損失の場合($R=G=0$)の電信方程式は
$$
\frac{\partial^2 v}{\partial x^2} = LC \frac{\partial^2 v}{\partial t^2} , ~
\frac{\partial^2 i}{\partial x^2} = LC \frac{\partial^2 i}{\partial t^2}
$$
で表され,波動方程式の形になる.
ここで,電信方程式の元となった分布定数回路の基礎方程式は
$$
-\frac{\partial v}{\partial x} = R i + L \frac{\partial i}{\partial t}, ~
-\frac{\partial i}{\partial x} = G v + C \frac{\partial v}{\partial t}
$$
で表された.この方程式に$R=G=0$を代入すると,
$$
-\frac{\partial v}{\partial x} = L \frac{\partial i}{\partial t}, ~
-\frac{\partial i}{\partial x} = C \frac{\partial v}{\partial t}
$$
とより簡単な形で方程式が得られる.
よって,無損失の場合は上記の偏微分方程式を解くことで電流と電圧の解を得ることができる.
以下では,この方程式の解の導出を行う.
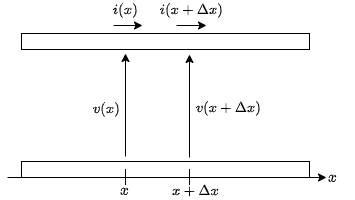
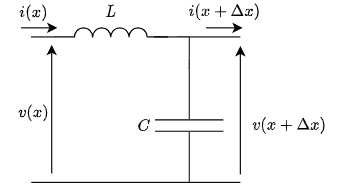
無損失の場合の電信方程式の解の導出
上記の方程式を行列の形で書き直すと次のようになる.
$$
-\frac{\partial}{\partial x}
\left(
\begin{array}{c}
v \\ i \\
\end{array}
\right) =
\left(
\begin{array}{cc}
0 & L \\ C & 0 \\
\end{array}
\right)
\frac{\partial}{\partial x}
\left(
\begin{array}{c}
v \\ i \\
\end{array}
\right) .
$$
この方程式を対角化を用いて簡単化することを考える.
右辺の行列の固有値$\lambda_1, \lambda_2$ とすると
$$
\lambda_1 = \sqrt{LC}, ~\lambda_2= -\sqrt{LC}
$$
となり,対応する固有ベクトルは$v_1, ~ v_2$ は
$$
v_1 =
\left(
\begin{array}{c}
1 \\ \sqrt{\frac{C}{L}} \\
\end{array}
\right), ~
v_2 =
\left(
\begin{array}{c}
1 \\ -\sqrt{\frac{C}{L}} \\
\end{array}
\right)
$$
と計算できる.よって,
$$
P = (v_1|v_2) =
\left(
\begin{array}{cc}
1 & \sqrt{\frac{C}{L}} \\
1 & -\sqrt{\frac{C}{L}} \\
\end{array}
\right)
$$
とおけば,
$$
P^{-1}AP =
\left(
\begin{array}{cc}
\sqrt{LC} & 0 \\
0 & -\sqrt{LC} \\
\end{array}
\right)
$$
と対角化できる.
左から$P^{-1}$をかけた後,$P P^{-1} = E$であることを利用し$\partial/\partial t$ を挟んで挿入すると,
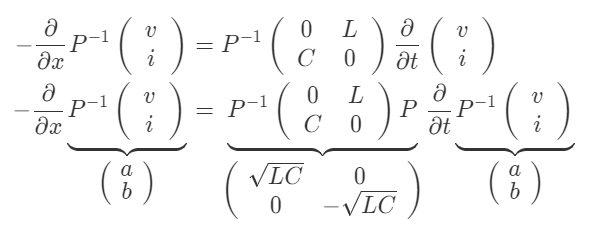
と整理できるので,変数変換を用いると,
$$
-\frac{\partial}{\partial x}
\left( \begin{array}{c} a \\ b \\ \end{array} \right) =
\left(
\begin{array}{cc}
\sqrt{LC} & 0 \\ 0 & -\sqrt{LC} \\
\end{array}
\right)
\frac{\partial}{\partial t}
\left( \begin{array}{c} a \\ b \\ \end{array} \right)
\label{eq:ab}
$$
とできる.
ここで$(a ~b)^{\rm T}$は,
$$
\left( \begin{array}{c} a \\ b \\ \end{array} \right)
= P^{-1} \left( \begin{array}{c} v \\ i \\ \end{array} \right)
$$
としている.
さらに,$x, ~t$について次のように変数変換を行う.
$$
x + \frac{t}{\sqrt{LC}} = \xi, ~ x – \frac{t}{\sqrt{LC}} = \eta
$$
とする.$a$を$x$ または$t$ で偏微分したときを考えると
$$
\begin{aligned}
\frac{\partial a}{\partial x} &=
\frac{\partial a}{\partial \xi} \cdot \frac{\partial \xi}{\partial x}
+\frac{\partial a}{\partial \eta} \cdot \frac{\partial \eta}{\partial x}
= \frac{\partial a}{\partial \xi} +\frac{\partial a}{\partial \eta} \\
\frac{\partial a}{\partial t} &=
\frac{\partial a}{\partial \xi} \cdot \frac{\partial \xi}{\partial t}
+\frac{\partial a}{\partial \eta} \cdot \frac{\partial \eta}{\partial x}
= \frac{1}{\sqrt{LC}} \left( \frac{\partial a}{\partial \xi} – \frac{\partial a}{\partial \eta} \right)
\end{aligned}
$$
のように求められる.これを式\eqref{eq:ab}に代入し計算すると,
$$
\frac{\partial a}{\partial \xi} = 0, ~ \frac{\partial b}{\partial \eta} = 0
$$
の関係が導かれる.なので,$f_1, ~ f_2$を任意関数として
$$
\begin{aligned}
a &= f_1(\eta) = f_1(x-\frac{1}{\sqrt{LC}}t) \\
b &= f_2(\xi) = f_2(x+\frac{1}{\sqrt{LC}}t)
\end{aligned}
$$
とできる(補足参照).
したがって,
$$
\left( \begin{array}{c} v \\ i \\ \end{array} \right)
= P \left( \begin{array}{c} a \\ b \\ \end{array} \right)
= \left( \begin{array}{c} f_1(x-\frac{1}{\sqrt{LC}}t) + f_2(x+\frac{1}{\sqrt{LC}}t) \\ \sqrt{\frac{C}{L}} f_1(x-\frac{1}{\sqrt{LC}}t) – \sqrt{\frac{C}{L}} f_2(x+\frac{1}{\sqrt{LC}}t) \\ \end{array} \right)
$$
と解を求めることができる.
これはダランベールの解と呼ばれる.
- 補足 偏微分が0から何が言えるか
$$
\frac{\partial}{\partial \xi} a(\xi, \eta) = 0
$$
のとき,両辺$\xi$で積分すると,
$$
\int_{\xi_0}^{\xi_1} \frac{\partial}{\partial \xi} a(\xi, \eta)
= a(\xi_1, \eta) – a(\xi_0, \eta) = 0
$$
が成立すればよく,これは $\underline{a}$が$\xi$を含まない場合であれば良いので,
$$
a=f(\eta)
$$
のように,残りの変数(今回の場合は$\eta$)のみが含まれる任意の関数となる.
まとめ
無損失線路の電信方程式について解の導出法を紹介した.
この方程式の解はダランベールの解となり,次のように進行波と後退波の和の形で表される.
$$
\left( \begin{array}{c} v \\ i \\ \end{array} \right)
= P \left( \begin{array}{c} a \\ b \\ \end{array} \right)
= \left( \begin{array}{c} f_1(x-\frac{1}{\sqrt{LC}}t) + f_2(x+\frac{1}{\sqrt{LC}}t) \\ \sqrt{\frac{C}{L}} f_1(x-\frac{1}{\sqrt{LC}}t) – \sqrt{\frac{C}{L}} f_2(x+\frac{1}{\sqrt{LC}}t) \\ \end{array} \right)
$$