この記事では,関数補完法として知られるラグランジュ(Lagrange)の補間法,ニュートン(Newton)の補間法について述べる.
また,python のサンプルコードで理解を深める.
関数補間
離散的なサンプルデータが得られたとき,これらの値を全て満たす曲線を求めて,中間の値を補間することを関数補間と言う.
例えば,$n$ 点のデータが得られているときは,$n-1$ 次式の多項式によって,全ての点を通る曲線を表せる.
離散データが$(x_0, y_0), (x_1, y_1), (x_2, y_2)$ の3点のとき,これらの点を通る曲線は
$$y = \alpha x^2 + \beta x + \gamma $$
のように,2次の多項式で表される.
これらに $(x_0, y_0), (x_1, y_1), (x_2, y_2)$ を代入すると,
$$
\begin{aligned}
{x_0}^2 \alpha + x_0 \beta + \gamma = y_0 \\
{x_1}^2 \alpha + x_1 \beta + \gamma = y_1 \\
{x_2}^2 \alpha + x_2 \beta + \gamma = y_2
\end{aligned}
$$
となり,$\alpha, \beta, \gamma$ の連立方程式を解くことで3点を全て通る多項式を得られる.
しかし,サンプル数が3点よりも多い $n$ 点の場合は,計算コストが高い.
そこで,$\alpha, \beta, \cdots$ などの係数を直接的に求める方法として,ラグランジュの補間法とニュートンの補間法が知られている.
ラグランジュの補間法
離散データが $(x_0, y_0), (x_1, y_1), \cdots, (x_n, y_n)$ の $n$ 点のとき,これらの点を通る直線は
$$y=\alpha_0 x^n + \alpha_1 x^{n-1} + \cdots + \alpha_{n-1} x + \alpha_n $$
のように $n$ 次の多項式で表されるが,これに $(x_0, y_0), (x_1, y_1), \cdots, (x_n, y_n)$ を代入し,多次元の連立方程式を解く方法は計算コストが大きい.
そこで,ラグランジュの補間法では多項式の置き方を工夫する.
ラグランジュの補間法では,次のように多項式を置く.
$$
\begin{aligned}
y &= y_0 z_0 + y_1 z_1 + \cdots + y_{n-1} z_{n-1} + y_n z_n \\
z_0 &= ~~ \qquad \qquad \dfrac{x-x_1}{x_0-x_1} \cdot \dfrac{x-x_2}{x_0-x_2} \cdots \dfrac{x-x_n}{x_0-x_n} \\
z_1 &= \dfrac{x-x_0}{x_1-x_0} \cdot \qquad \qquad \cdot ~ \dfrac{x-x_2}{x_1-x_2} \cdots \dfrac{x-x_n}{x_1-x_n} \\
z_2 &= \dfrac{x-x_0}{x_2-x_0} \cdot \dfrac{x-x_1}{x_2-x_1} \cdot \qquad \qquad \cdots \dfrac{x-x_n}{x_0-x_n} \\
\vdots \\
z_n &= \dfrac{x-x_0}{x_n-x_0} \cdot \dfrac{x-x_1}{x_n-x_1} \cdot \dfrac{x-x_2}{x_n-x_2} \cdots
\end{aligned}
$$
$z$ の形は次に示す
$$\dfrac{x-x_0}{x_k-x_0} \cdot \dfrac{x-x_1}{x_k-x_1} \cdot \dfrac{x-x_2}{x_k-x_2} \cdots \dfrac{x-x_n}{x_k-x_n}$$
から,添え字が同じ項を消去した形になっている.
$z_k$ は全て $x$ の $n-1$ 次式であるので,これらの和も $n-1$ 次式になる.
上記の多項式が $(x_0, y_0), (x_1, y_1), \cdots, (x_n, y_n)$ を全て通ることはすぐに確認できる.
例えば,$x = x_0$ とすると,
$$
\begin{aligned}
z_0 = 1 \\
z_1 = z_2 = \cdots = z_n = 0
\end{aligned}
$$
となるため,$y = y_0$ となり,$(x_0, y_0)$ を通ることを確認できる.
また,$x_1, x_2, \cdots x_n$ を代入したときも,同様の結果が得られるため,
上記の多項式は $(x_0, y_0), (x_1, y_1), \cdots, (x_n, y_n)$ を全て通る曲線である.
よって,上記のような多項式を直接計算することで,関数補間を行える.
Python によるサンプルコード
import numpy as np
import matplotlib.pyplot as plt
## ------ params ------ ##
x_ary = np.array([0.0, 1.0, 2.0, 2.5, 4.1, 5.0])
xplot_ary= np.linspace(x_ary[0], x_ary[-1], 100)
y_ary = np.array([0.0, 1.1, 2.5, 4.0, 4.1, 5.0])
## ------ function ------ ##
def lagrange(x_ary, xn_ary, yn_ary):
dim = len(xn_ary)
## calculate denominator
xn_mat = np.tile(xn_ary, (dim, 1))
denominator_mat = xn_mat.T - xn_mat
## prevent dividing by 0
denominator_mat[np.diag_indices(dim)] = 1
y_ary = np.empty(0)
for i in range(len(x_ary)):
## calculate numerator
x_mat = np.tile(x_ary[i], (dim, dim))
numerator_mat = x_mat - xn_mat
## calculate zn
a_mat = numerator_mat / denominator_mat
a_mat[np.diag_indices(dim)] = 1
zn_ary = np.prod(a_mat, axis=1)
## calculate y
y = np.dot(yn_ary, zn_ary)
y_ary = np.hstack([y_ary, y])
return y_ary
## ------ main ------ ##
yplot_ary = lagrange(xplot_ary, x_ary, y_ary)
fig, ax = plt.subplots(figsize=(8,5))
fig.subplots_adjust(left=0.15, bottom=0.15)
ax.scatter(x_ary, y_ary)
ax.plot(xplot_ary, yplot_ary, '-k')
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
ax.grid()
plt.show()上記のサンプルコードからは次のような出力が得られる.
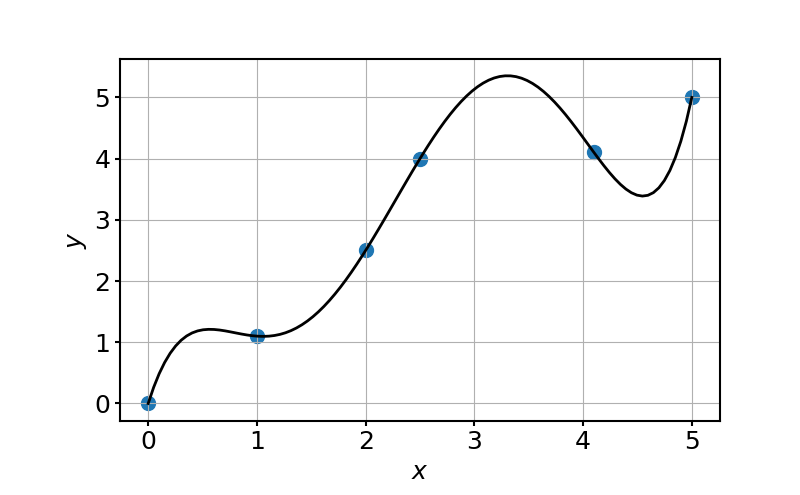
ニュートンの補間法
ラグランジュの補間法のように,多項式の置き方を工夫するもう1つの手法として,ニュートンの補間法がある.
ニュートンの補間法では,次のように多項式を置く.
$$
\begin{aligned}
y = a_0 &+ a_1 (x-x_0) + a_2 (x-x_0) (x-x_1) + \cdots \\
& \cdots + a_n (x-x_0) (x-x_1) \cdots (x-x_{n-1})
\end{aligned}
$$
上記の多項式に $(x_0, y_0), (x_1, y_1), \cdots, (x_n, y_n)$ を全て通るという条件を付けると,次に示す関係が成り立つ.
$$
\begin{aligned}
y_0 &= a_0 \\
y_1 &= a_0 + a_1(x_1-x_0) \\
y_2 &= a_0 + a_1(x_2-x_0) + a_2(x_2-x_0)(x_2-x_1) \\
\vdots \\
y_n &= a_0 + a_1(x_2-x_0) + \cdots + a_2(x_n-x_0) \cdots (x_n-x_{n-1})
\end{aligned}
$$
この連立方程式は,1式目で求まった$a_0$ を2式目に代入することで$a_1$ が求まり,これらの $a_0, a_1$ を3式目に代入すると $a_2$ が求まる.
このように,再帰的な操作で係数 $a_k$ が求まるため,多項式の係数を計算するコストを下げることができる.
この式を $a_0, a_1, \cdots$ について解いていくと,
$$
\begin{aligned}
a_0 &= y_0 \\
a_1 &= \frac{y_1 – y_0}{x_1 – x_0} \\
a_2 &= \frac{\frac{y_2 – y_1}{x_2 – x_1} – \frac{y_1 – y_0}{x_1 – x_0}}{x_2 – x_0} \
a_3 &= \frac{ \frac{\frac{y_3 – y_2}{x_3 – x_2} – \frac{y_2 – y_1}{x_2 – x_1}}{x_3 – x_1} – \frac{\frac{y_2 – y_1}{x_2 – x_1} – \frac{y_1 – y_0}{x_1 – x_0}}{x_2 – x_0} }{x_3-x_0} \\
\vdots
\end{aligned}
$$
のようになる.
$a_0, a_1, \cdots$の解の形は差分商と呼ばれる.
差分商は次のように定義できて
$$
\begin{aligned}
f[x_1, x_0] &= \frac{y_1 – y_0}{x_1 – x_0} \\
f[x_2, x_1, x_0] &= \frac{\frac{y_2 – y_1}{x_2 – x_1} – \frac{y_1 – y_0}{x_1 – x_0}}{x_2 – x_0} = \frac{f[x_2, x_1]-f[x_1, x_0]}{x_2-x_0} \\
f[x_k, x_{k-1}, \cdots, x_1, x_0] &= \frac{f[x_k, x_{k-1}, \cdots, x_2, x_1]-f[x_{k-1}, x_{k-2}, \cdots, x_1, x_0]}{x_k-x_0} \\
\end{aligned}
$$
のような形になる.
数値計算上は,2次元配列に,
$$
\begin{pmatrix}
y_0 & f[x_1, x_0] & f[x_2, x_1, x_0] & f[x_3, x_2, x_1, x_0] & f[x_4, x_3, x_2, x_1, x_0] \\
y_1 & f[x_2, x_1] & f[x_3, x_2, x_1] & f[x_3, x_2, x_1, x_0] & 0 \\
y_2 & f[x_3, x_2] & f[x_4, x_3, x_2] & 0 & 0 \\
y_3 & f[x_4, x_3] & 0 & 0 & 0 \\
y_4 & 0 & 0 & 0 & 0
\end{pmatrix}
$$
のように計算して行く手法が取られ,第1列目である
$$
y_0, f[x_1, x_0], f[x_2, x_1, x_0], f[x_3, x_2, x_1, x_0], f[x_4, x_3, x_2, x_1, x_0]
$$
が係数 $a_k$ となる.
Python によるサンプルコード
次にニュートンの補間法のサンプルコードを示す.
import numpy as np
import matplotlib.pyplot as plt
## ------ params ------ ##
x_ary = np.array([0.0, 1.0, 2.0, 2.5, 4.1, 5.0])
xplot_ary= np.linspace(x_ary[0], x_ary[-1], 100)
y_ary = np.array([0.0, 1.1, 2.5, 4.0, 4.1, 5.0])
## ------ function ------ ##
def newton(x_ary, xn_ary, yn_ary):
dim = len(yn_ary)
coef_mat = np.zeros([dim, dim])
## substitute the first column yn
coef_mat[:, 0] = yn_ary
## calculate divided difference
for j in range(1,dim):
for i in range(dim-j):
coef_mat[i][j] = (coef_mat[i+1][j-1]\
- coef_mat[i][j-1]) / (xn_ary[i+j]-xn_ary[i])
an_ary = coef_mat[0, :]
## calculate yplot
y_ary = np.empty(0)
for i in range(len(xplot_ary)):
## calculte (x-xn)
x_xn_ary = np.roll(x_ary[i] - xn_ary, 1)
x_xn_ary[0] = 1.0
## (x-x0), (x-x0)(x-x1), (x-x0)(x-x1)(x-x2), ...
xCumProd_ary = np.cumprod(x_xn_ary)
y = np.dot(an_ary, xCumProd_ary)
y_ary = np.hstack([y_ary, y])
return y_ary
## ------ main ------ ##
yplot_ary = newton(xplot_ary, x_ary, y_ary)
fig, ax = plt.subplots(figsize=(8,5))
fig.subplots_adjust(left=0.15, bottom=0.15)
ax.scatter(x_ary, y_ary)
ax.plot(xplot_ary, yplot_ary, '-k')
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
ax.grid()
plt.show()上記のサンプルコードからは次のような出力が得られる.
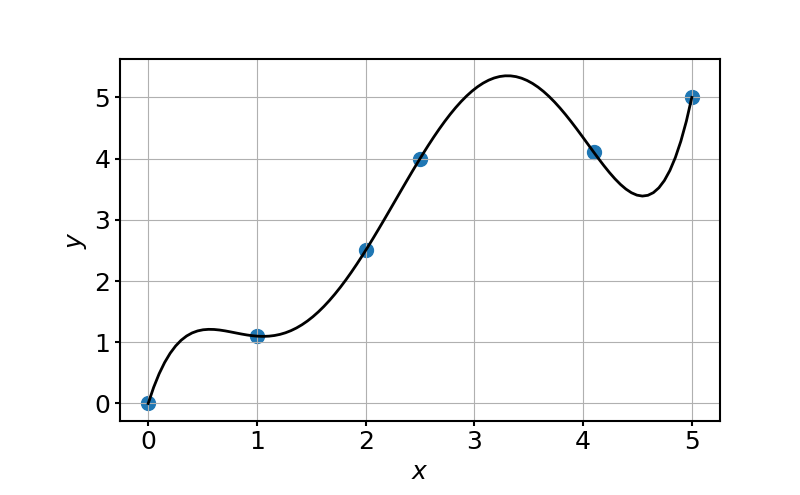
参考
[1] 三井田 惇郎,須田 宇宙,数値計算法[第2版],森北出版,2014
[2] Newton’s Polynomial Interpolation,
https://pythonnumericalmethods.berkeley.edu/notebooks/chapter17.05-Newtons-Polynomial-Interpolation.html




