この記事では,離散フーリエ変換(DFT:Discrete Fourier Transform)の簡単な説明とこれを高速化した高速フーリエ変換(FFT:Fast Fourier Transform)のアルゴリズムについて書き,pythonで実装し理解を深める.
離散フーリエ変換(DFT)
離散フーリエ変換(DFT:Discrete Fourier Transform)は時間領域から周波数領域に変換するフーリエ変換の離散verである.
DFTで解析する信号は,基本的には周期的な信号である必要がある.
ある信号$f$の1周期分をM点サンプリングを行うと,$f[0], f[1], \cdots, f[M-1]$が得られる.
その$i$番目のデータは,複素フーリエ級数として知られている通り,次のように複素正弦波群の和の形で表せる.
$$f[i] = \sum_{k=0}^{M-1} F[k] e^{-j \left( \frac{2 \pi i}{M} \right) k} \label{eq:IDFT}$$
この係数$F[0], F[1], \cdots, F[M-1]$は,各周波数成分を表すもので,これらの係数は次の式のようにDFTを行うことで求められる.
$$F[i] = \frac{1}{M}\sum_{i=0}^{M-1} f[i] e^{-j \left( \frac{2 \pi k}{M} \right) i}$$
DFTでは,1つの要素$F[i]$を計算するのに$M$個の計算結果を足し合わせるため,$M$回演算が必要になる.
また,$F$は$M$個の要素があるので,上記の演算を$M$回繰り返す必要があり,サンプリング点数$M$に対して演算回数は$M^2$回必要となる.
DFTの例
上記の説明では抽象的なので,既に関数の形が分かっている関数に対してDFTを行ってみる.
今回は例として次のような関数$f$を対象としよう.
$$f(x) = 3 \sin{x} + 7 \cos{x} \label{eq:f}$$
この関数を$1$周期$2 \pi$の間に$M$回サンプリングする.
この場合,サンプリング周期は $T = 2 \pi/M$ になるので,$i$回目のサンプリング時の$x$は
$$x = \frac{2 \pi i}{M}$$
になる.
以上を図示すると次のようになる.
サンプリング数を $M=8$ とし,黒点はサンプリング点を表している.
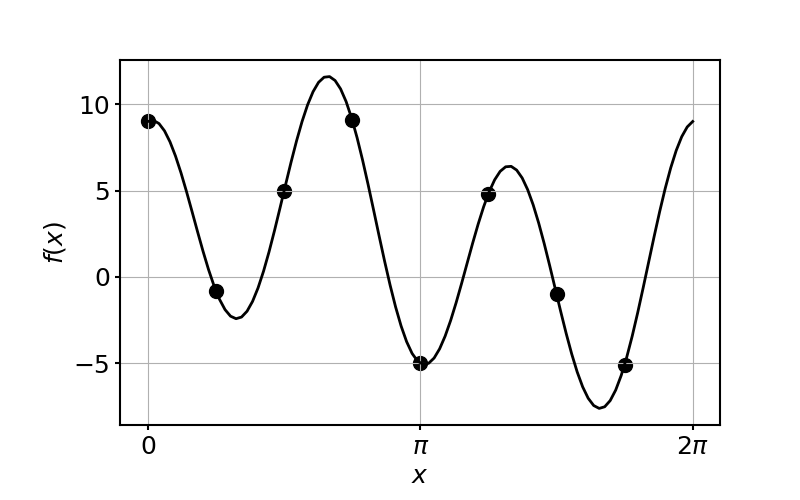
これを下記で示すコードで計算すると$F[k]$は表のとおりになる.
| k | 対応周波数[Hz] | 対応角周波数[rad/s] | 実部 | 虚部 |
|---|---|---|---|---|
| 0 | D.C | D.C. | 2.0 | 0.0 |
| 1 | $1/2 \pi$ | 1 | 0.0 | -1.5 |
| 2 | $1/ \pi$ | 2 | 0.0 | 0.0 |
| 3 | $3/2 \pi$ | 3 | 3.5 | 0.0 |
| 4 | $2/ \pi$ | 4 | 0.0 | 0.0 |
| 5 | $-3/2\pi$ | -3 | 3.5 | 0.0 |
| 6 | $-1/ \pi$ | -2 | 0.0 | 0.0 |
| 7 | $-1/2\pi$ | -1 | 0.0 | 1.5 |
重要な点として,
- サンプリング周波数の半値(ナイキスト周波数) 以上の対応周波数は負の周波数になる.
これは扇風機を見たときに逆回転しているように見える原理で,サンプリング周波数の半値以上の信号は逆に動いているように見えることを意味する. - $k = n, M-n ~(n=1, 2, \cdots, M/2-1)$ のDFT結果 $F[k]$ は共役複素数の関係になる (※$n=0$を除いていることに注意).
この対応がなければ,次に行う検算において,信号$f$に虚数が残ってしまうことから確認できる.
この結果を式\eqref{eq:IDFT}に代入すれば,元の信号$f$に戻るはず.
これを検算してみる.
$$
\begin{aligned}
f[i] &= \sum_{k=0}^{M-1} F[k] e^{-j \left( \frac{2 \pi i}{M} \right) k} \\
&= F[0] e^{-j \left( \frac{2 \pi i}{M} \right) 0} \rightarrow 2.0 \\
& + F[1] e^{-j \left( \frac{2 \pi i}{M} \right) 1} + F[0] e^{-j \left( \frac{2 \pi i}{M} \right) 7} \rightarrow 3 \sin{\frac{2 \pi i}{M}} \\
& + F[0] e^{-j \left( \frac{2 \pi i}{M} \right) 3} + F[0] e^{-j \left( \frac{2 \pi i}{M} \right) 5} \rightarrow 7 \cos{\frac{2 \pi i}{M}}\\
\end{aligned}
$$
よって,元の信号になることが確認できる.
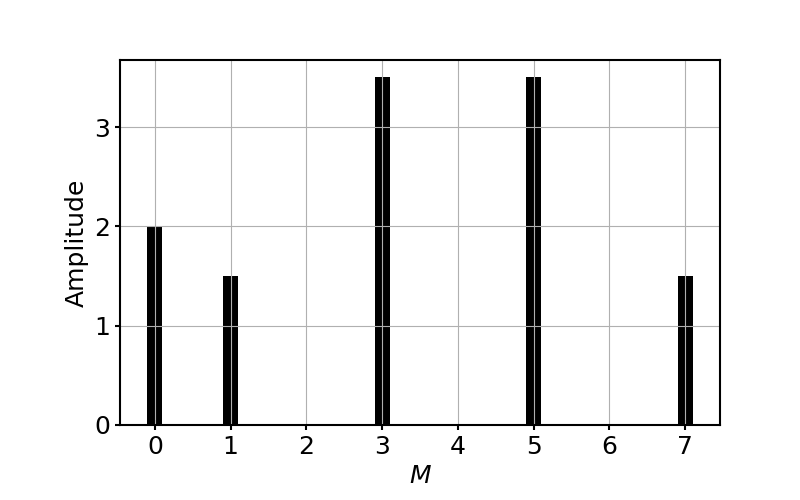
絶対値$|F[i]|$を計算すると次のようにスペクトルが確認できる.
DFTのコードサンプル(Python)
上記の計算に用いたサンプルコードについて説明する.
まず,関数$f$及び各パラメータの定義
def func(x):
return 3*np.sin(x) + 7*np.cos(3*x)P = 16
N = np.arange(0, P)
x = 2*np.pi*N/PDFTは次のようなコードで実装できる.
Numpyは複素数の計算をサポートしているので,容易に実装できる.
import numpy as np
Amp = np.empty(0)
for M in range(P):
fNexp = func(x) * np.exp(1j*-x*M)
aM = np.sum(fNexp) / P
print('{:.3f}'.format(aM))
Amp = np.hstack([Amp, np.abs(aM)])また,numpyにはfftが関数として予めあるので,普通はこれを使う.
上記のコードと下のコードは同等.
import numpy as np
fft = np.fft.fft(func(x)) / M
Amp = np.abs(npfft)高速フーリエ変換(FFT)のアルゴリズム
DFTはサンプリング点数$M$に対して演算回数は$M^2$回必要となり,点数が多くなると処理時間が長くなる.
これを改善したのがFFTで,計算回数は $(M/2) \log_2 M$ 回に抑えられ,処理時間を短くできる.
$M=2^{10}=1024$ のときでは,乗算回数は約 1/200 に抑えられる.
時間分割法
それでは,FFTの具体的なアルゴリズムの話に移る.
FFTのポピュラーなアルゴリズムとしては,時間分割法を用いたものが知られている.
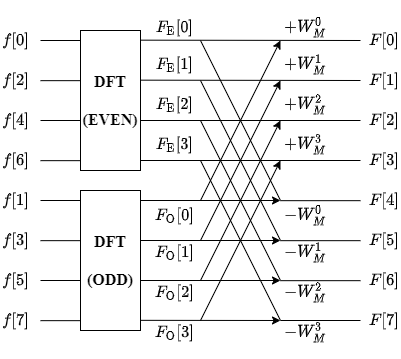
時間分割法は,次の図のようにサンプリング点を偶数列と奇数列に分割してFFTをかけ,それらの結果から元の信号のFFT結果を求める方法である.
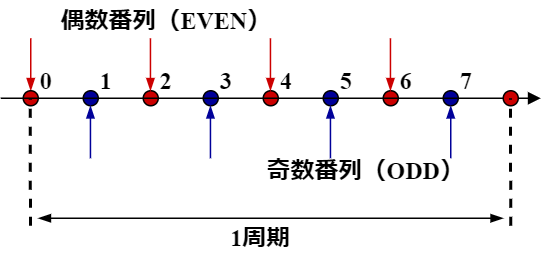
偶数と奇数列に分けることで乗算回数を $2\cdot (M/2)^2 = M^2/2$ に減らすことができる.
ここで問題となるのは,
偶数列,奇数列のFFT結果から元の信号のFFT結果を知る方法 である.
それは,次のようにFFTの式から,偶数列と奇数列に分割した形で表すことで分かる.
$$
\begin{aligned}
& \frac{1}{M} \sum_{i=0}^{M-1} f[i] e^{-j \left( \frac{2 \pi i}{M} \right) k} \\
&= \frac{1}{M} \sum_{l=0}^{(M-2)/2} f[2l] e^{-j \left( \frac{2 \pi (2l)}{M} \right) k} + \frac{1}{M} \sum_{l=0}^{(M-2)/2} f[2l+1] e^{-j \left( \frac{2 \pi (2l+1)}{M} \right) k}
\\
&= \frac{1}{M} \sum_{l=0}^{(M-2)/2} f[2l] e^{-j \left( \frac{2 \pi l}{M/2} \right) k} + e^{-j \left( \frac{2 \pi k}{M} \right)} \frac{1}{M} \sum_{l=0}^{(M-2)/2} f[2l+1] e^{-j \left( \frac{2 \pi l}{M/2} \right) k}
\end{aligned}
$$
上式の $(1/M) \cdot \sum$ は,それぞれ偶数列と奇数列にFFTを行う数式となっている.
これより,偶数列信号(EVEN)のFFT結果を$F_{\rm E}$,奇数列信号(ODD)のFFT結果を$F_{\rm O}$とすると
$$F[k] = F_{\rm E}[k] + e^{-j \left( \frac{2 \pi k}{M} \right)} F_{\rm O}[k] ~~(k=0, 1, 2. \cdots , (M-2)/2) \label{eq:evenodd}$$
となる.
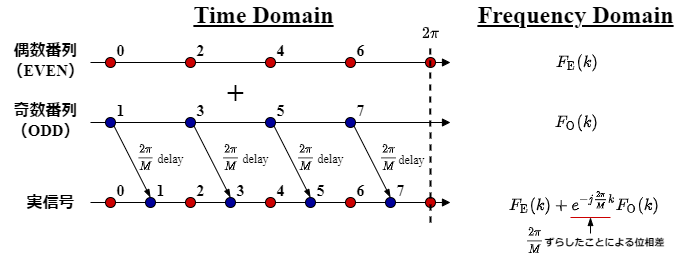
物理的には,FFT時点では奇数列は$t=0$として扱われているが,実際は奇数列は偶数列から$2\pi /M$の時間だけ遅延したものである.
よって,この時間遅延が周波数領域では位相差として現れているのである.
また,$k = n, M-n ~(n=1, 2, \cdots, M/2-1)$ のDFT結果 $F[k]$ は共役複素数の関係になるので,
$$
\begin{aligned}
F[M-n] &= \bar{F}[n] \\
& = \bar{F_{\rm E}} [n]- e^{j \left( \frac{2 \pi k}{M} \right)} \bar{F_{\rm O}}[k] \\
& = \bar{F_{\rm E}} [M/2-n]- e^{j \left( \frac{2 \pi k}{M} \right)} \bar{F_{\rm O}}[M/2-n]
\end{aligned}
$$
のように導けるから,$k=M/2-n$ と置き直して,
$$F[k+M/2] = F_{\rm E}[k] – e^{-j \left( \frac{2 \pi k}{M} \right)} F_{\rm O}[k] ~~(k=0, 1, 2. \cdots , (M-2)/2)$$
とできる.
まとめると,$k=0, 1, 2. \cdots , (M-2)/2$に対して
$$
\begin{aligned}
F[k] &= F_{\rm E}[k] + e^{-j \left( \frac{2 \pi k}{M} \right)} F_{\rm O}[k] \\
F[k+M/2] &= F_{\rm E}[k] – e^{-j \left( \frac{2 \pi k}{M} \right)} F_{\rm O}[k]
\end{aligned}
$$
となる.
この結果より,偶数列と奇数列それぞれに対してFFTをかけ,次の図のように演算を乗算及び加算を行うことで,もとの信号に対するFFT結果を得ることができる.
この演算はバタフライ演算として知られている.
※図においては,$W_M^k = e^{2 \pi k / M}$と置いた.
ビット逆順によるデータの並び替えとバタフライ演算
上記で説明した時間分割法は,データ数に$M=2^n$($n$は正の整数) という条件を付した場合は,$n-1$ 回だけ同じ操作を行える.
これによって,サンプル数が $2^n$ の場合,最終的に2データの組が $2^{n-1}$ 個できる.
$M=2^3=8$ の場合は,次のように2データの組が4つできる.
$$
\begin{aligned}
(f[0], f[1], f[2], f[3], f[4], f[5], f[6], f[7]) \nonumber \\
(f[0], f[2], f[4], f[6]), (f[1], f[3], f[5], f[7]) \\
(f[0], f[4]), (f[2], f[6]), (f[1], f[5]), (f[3], f[7]) \nonumber \\
\end{aligned}
$$
このデータの並び替えはビット逆順によって得られる.
ビット逆順とは次のように,10進数を2進数にしてビット列を逆順にすることだ.
| 10進数 | 2進数 | ビット逆順 | 10進数(逆順後) |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |
このようにビット逆順に並び替えた後,得られる2データ群のそれぞれに対してFFTを行い,式\eqref{eq:evenodd} の計算を再帰的に行うことで,元の信号のFFT結果を得ることができる.
具体的な手順を次に示す.
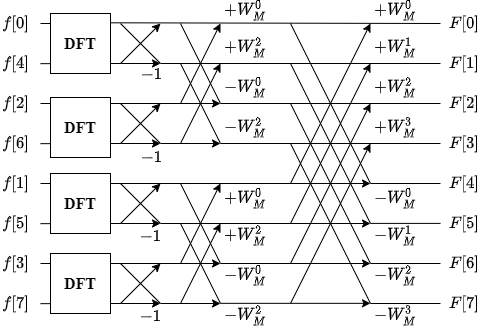
この演算によって,FFTにおける乗算は $2M$ 回になる.
また,バタフライ演算における乗算回数は$(P/2)\log_2 {P}$ 回に抑えられる.
参考文献
[1] 三井田 惇郎,須田 宇宙,数値計算法[第2版],森北出版,2014




