この記事では,逆行列の数値計算法について説明する.
また,python のサンプルコードで理解を深める.
掃き出し法を用いたアルゴリズム
逆行列を求める手法として掃き出し法を用いた方法がある.
今回は行列 $\boldsymbol{A}$ は正方行列としてこの逆行列 $\boldsymbol{A}^{-1}$を求める.
図においては,$\boldsymbol{A}$ は3×3行列とした.
$\boldsymbol{A}$ の要素を $a_{ij}$とし,$\boldsymbol{A}^{-1}$ の要素を $x_{ij}$ とすると,
$$
\begin{aligned}
\boldsymbol{A} \boldsymbol{A}^{-1} &= \boldsymbol{I} \\
\begin{pmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{pmatrix}
\begin{pmatrix}
x_{11} & x_{12} & x_{13} \\
x_{21} & x_{22} & x_{23} \\
x_{31} & x_{32} & x_{33}
\end{pmatrix} &=
\begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{pmatrix}
\end{aligned}
$$
この行列式は分解すると,次のように 3 個の 3元連立方程式になる.
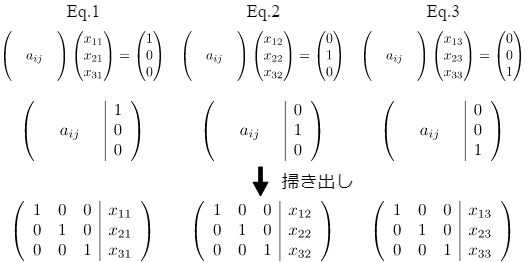
よって,逆行列はこれらの方程式の解をすべて求めることで計算できる.
$n$ 元連立方程式は,ガウス・ジョルダン法 (掃き出し法) で解を求めることができる.
$3$元連立方程式の場合,係数行列$a_{ij}$ に係数列($(1 0 0)^T, (0 1 0)^T, (0 0 1)^T$) をくっつけて,それぞれの場合について掃き出し法を行えば良い.
※ガウス・ジョルダン法(掃き出し法) については次を参照
ただし,1つの連立方程式に掃き出し法を適用し,これを $n$ 回繰り返すのは非効率である.
そこで,次から説明するように係数行列 $a_{ij}$ に単位行列 $\boldsymbol{I}$ を右に結合して付加行列を作り,掃き出し法を行うことで $n$ 個の連立方程式を一度に解くことができ,逆行列を求めることができる.
まず,係数行列 $a_{ij}$ に単位行列 $\boldsymbol{I}$ を右に結合して付加行列を作る.
$$
\begin{aligned}
\left(
\begin{array}{ccccc|ccccc}
a_{11} & a_{12} & a_{13} & \cdots & a_{1n} & 1 & 0 & 0 & \cdots & 0\\
a_{21} & a_{22} & a_{23} & \cdots & a_{2n} & 0 & 1 & 0 & \cdots & 0\\
a_{31} & a_{32} & a_{33} & \cdots & a_{3n} & 0 & 0 & 1 & & \vdots\\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots & & & \ddots & 0\\
a_{31} & a_{32} & a_{33} & \cdots & a_{nn} & 0 & 0 & \cdots & 0 & 1\\
\end{array}
\right)
\end{aligned}
$$
次に,第1行をピボット数 ($a_{11}$) で割り,1行目の定数倍を引くことでその他の第1列を消去する.
$$ \begin{aligned} \left( \begin{array}{ccccc|ccccc} 1 & a’_{12} & a’_{13} & \cdots & a’_{1n} & b’_{11} & 0 & 0 & \cdots & 0\\ 0 & a’_{22} & a’_{23} & \cdots & a’_{2n} & b’_{21} & 1 & 0 & \cdots & 0\\ 0 & a’_{32} & a’_{33} & \cdots & a’_{3n} & b’_{31} & 0 & 1 & & \vdots\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & & & \ddots & 0\\ 0 & a’_{32} & a’_{33} & \cdots & a’_{nn} & b’_{n1} & 0 & \cdots & 0 & 1\\ \end{array} \right) \end{aligned} $$同様に,第1行をピボット数 ($a’_{22}$) で割り,1行目の定数倍を引くことでその他の第1列を消去する.
$$ \begin{aligned} \left( \begin{array}{ccccc|ccccc} 1 & 0 & a’_{13} & \cdots & a’_{1n} & b’_{11} & b’_{12} & 0 & \cdots & 0\\ 0 & 1 & a’_{23} & \cdots & a’_{2n} & b’_{21} & b’_{22} & 0 & \cdots & 0\\ 0 & 0 & a’_{33} & \cdots & a’_{3n} & b’_{31} & b’_{32} & 1 & & \vdots\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & & \ddots & 0\\ 0 & 0 & a’_{33} & \cdots & a’_{nn} & b’_{n1} & b’_{n2} & \cdots & 0 & 1\\ \end{array} \right) \end{aligned} $$上記の操作を繰り返すことで,次の形の行列が得られる.
$$
\begin{aligned}
\left(
\begin{array}{ccccc|ccccc}
1 & 0 & 0 & \cdots & 0 & & \qquad & & \qquad & \\
0 & 1 & 0 & \cdots & 0 & & \qquad & & \qquad & \\
0 & 0 & 1 & \cdots & \vdots & & \qquad & b_{ij} & \qquad & \\
\vdots & \vdots & \vdots & \ddots & 0 & & \qquad & & \qquad & \\
0 & 0 & \cdots & 0 & 1 & & \qquad & & \qquad & \\
\end{array}
\right)
\end{aligned}
$$
この操作によって連立方程式の解が求められたことになり,右半分の $b_{ij}$ に逆行列が得られる.
Python スクリプト
次に掃き出し法に基づいた逆行列を計算する python のサンプルを示す.
import numpy as np
## ------ params ------ ##
A_mat = np.array([
[2.0, 1.0, 3.0],
[1.0, 3.0, 2.0],
[3.0, 2.0, 1.0]
])
eps = 1e-4
dim = A_mat.shape[0]
## ------ main ------ ##
I_mat = np.identity(dim)
Ai_mat = np.hstack([A_mat, I_mat])
print(Ai_mat)
for i in range(dim):
## judge pivot ~ 0
pivot = Ai_mat[i, i]
if np.abs(pivot) < eps:
print('pivot is near 0, exit')
exit()
else:
## divide by pivot
Ai_mat[i, :] = Ai_mat[i, :] / pivot
## row reduction
index = np.arange(dim)
for j in index[index != i]:
Ai_mat[j, :] = Ai_mat[j, :] - Ai_mat[j, i]*Ai_mat[i, :]
print(Ai_mat)
result = Ai_mat[:, -dim:]
print('result')
print(result)出力
上記のプログラムの出力結果を示す.
最後の result 以降の出力が逆行列の計算結果になっている.
[[2. 1. 3. 1. 0. 0.]
[1. 3. 2. 0. 1. 0.]
[3. 2. 1. 0. 0. 1.]]
[[ 1. 0.5 1.5 0.5 0. 0. ]
[ 0. 2.5 0.5 -0.5 1. 0. ]
[ 0. 0.5 -3.5 -1.5 0. 1. ]]
[[ 1. 0. 1.4 0.6 -0.2 0. ]
[ 0. 1. 0.2 -0.2 0.4 0. ]
[ 0. 0. -3.6 -1.4 -0.2 1. ]]
[[ 1. 0. 0. 0.05555556 -0.27777778 0.38888889]
[ 0. 1. 0. -0.27777778 0.38888889 0.05555556]
[-0. -0. 1. 0.38888889 0.05555556 -0.27777778]]
result
[[ 0.05555556 -0.27777778 0.38888889]
[-0.27777778 0.38888889 0.05555556]
[ 0.38888889 0.05555556 -0.27777778]]比較のために,numpy.linalg.inv を用いて求めたものと比較しよう.
print(np.linalg.inv(A_mat))行列やモジュールが定義済みとして,上記のコードを実行すると,
[[ 0.05555556 -0.27777778 0.38888889]
[-0.27777778 0.38888889 0.05555556]
[ 0.38888889 0.05555556 -0.27777778]]が得られ,一致していることが確認できる.
参考
[1] 三井田 惇郎,須田 宇宙,数値計算法[第2版],森北出版,2014




