FPの職業倫理,関連法規
FPの職業倫理
FPの職業倫理として次がある.
- 顧客の利益優先:顧客の利益を優先する資金プランニングを行う
- 守秘義務の順守:顧客の個人情報を許可なく第三者に伝えてはいけない
- 説明義務(アカウンタビリティ):顧客の知識レベルや経験に合わせ十分に説明
- 顧客の同意(インフォームドコンセント)
FPと関連法規
FP業務は保険業務や税務業務など様々な領域に渡るため,その他資格の独占業務を行わないよう注意が必要.
一般的な説明や家庭事例の説明はOK,個別具体的な相談や他の資格の独占業務はNGと覚えておく.
- FP業務と弁護士法
〇遺言の承認 ×個別具体的な法律判断,法律事務 - FP業務と税理士法
〇一般的な税法説明,仮定税額の計算 ×個別具体的な税務相談,税務書作成 - FP業務と金融商品取引法 ×投資判断:売買タイミングなど
金融商品取引業は内閣総理大臣の登録が必要(金融商品取引法) - FP業務と保険業法
〇一般的な商品説明,必要保証額計算 ×保険の募集や勧誘
ライフプランニングのツール
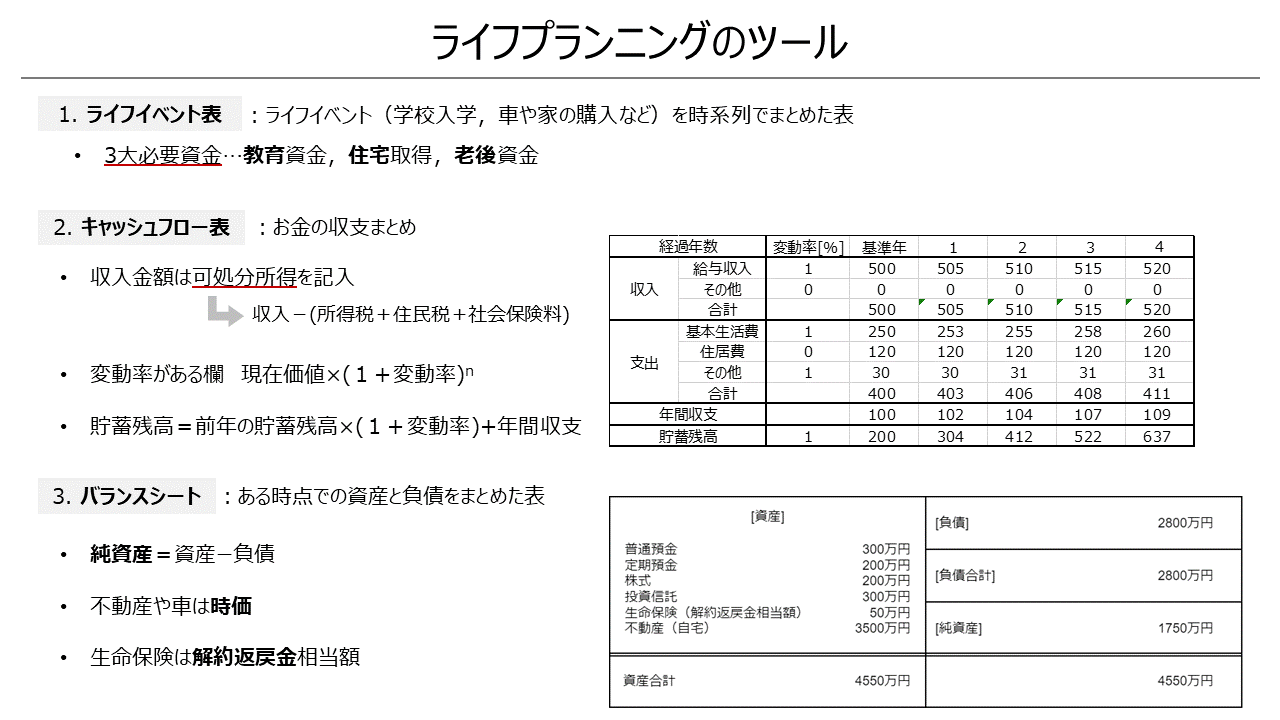
ライフイベント表
ライフイベントを時系列でまとめた表
関連して主なライフイベントである
3大必要資金(教育資金,住宅資金,老後資金)
を覚えておく
キャッシュフロー表
お金の収支を時系列でまとめたもの
注意点は次
- 収入金額は可処分所得を記入する
可処分所得=収入-(所得税+住民税+社会保険料) - 変動率がある欄 現在価値×(1+変動率)^n
- 貯蓄残高=前年の貯蓄残高×(1+変動率)+年間収支
バランスシート
ある時点での資産と負債をまとめた表.
純資産=資産ー負債 である.
次の点は頻出なので覚えておく.
- 不動産や車は時価で評価する
- 生命保険は解約返戻金相当額を資産とする
教育資金プランニング

教育資金の準備法としては主に次の3つ
- こども保険
- 教育ローン
- 奨学金
こども保険
こども保険は教育費用の貯蓄と保証を目的とした保険.
- 貯蓄機能…満期保険金や入学・進学時の祝い金
- 保証機能…親が死亡したとき以後の保険金が免除される
この場合,保険料を支払わなくても満期保険金や祝い金の受け取れることに注意
教育ローン
教育ローンには公的ローンと民間ローンがある.
代表的な公的ローンに教育一般貸付がある.
教育一般貸付の特徴は次のとおり.数字部分は頻出なので覚えておく.
- 融資限度額:学生1人あたり最高350万
- 固定金利
- 返済期間:最長18年
- 融資元:日本政策金融金庫
- 年収制限あり
奨学金
日本学生支援機構(JASSO)が提供している.
奨学金は一般的に学生本人が契約する.
奨学金の種類として次を覚えておく.
- 貸与型:第一種奨学金(無利息),第二種奨学金(有利息)
- 給付型:返済不要
住宅取得プランニング
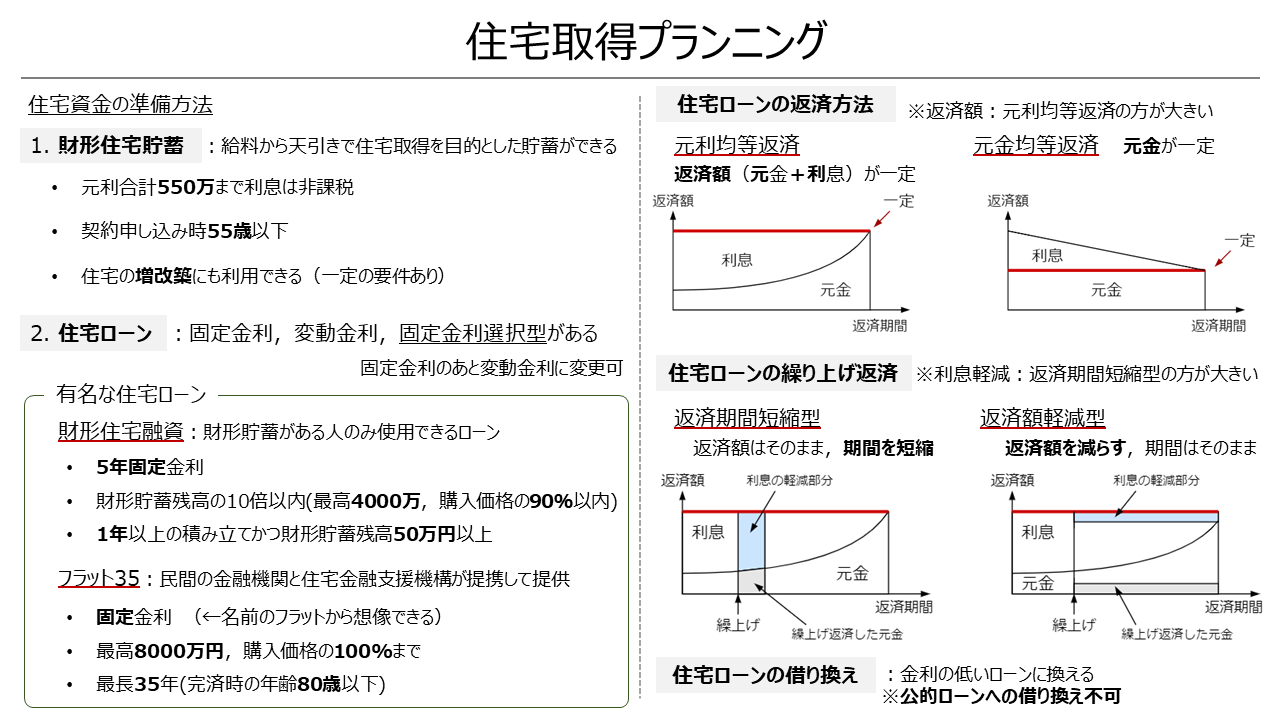
住宅資金の準備法としては次の2つ.
- 財形住宅貯蓄
- 住宅ローン
財形住宅貯蓄
給料から天引きで住宅取得を目的とした貯蓄ができる.
ただし,住宅取得以外には使えないので注意が必要.
その他の注意点は次のとおり.
- 元利合計550万まで利息は非課税
- 契約申し込み時55歳以下
- 住宅の増改築にも利用できる(一定の要件あり)
住宅ローン
住宅ローンには,固定金利,変動金利,固定金利選択型がある.
固定金利選択型は,固定金利の期間が過ぎたあとに固定金利か変動金利を選択できる住宅ローンである.
有名な住宅ローンに財形住宅融資とフラット35がある.
- 財形住宅融資:財形貯蓄がある人のみ使用できるローン
- 5年固定金利
- 財形貯蓄残高の10倍以内(最高4000万,購入価格の90%以内)
- 1年以上の積み立てかつ財形貯蓄残高50万円以上
- フラット35:民間の金融機関と住宅金融支援機構が提携して提供
- 固定金利 (名前のフラットから覚えておく)
- 最高8000万円,購入価格の100%まで
- 最長35年(フラット35という名前そのままで覚えておく)
- 完済時の年齢80歳以下
※財形貯蓄は,住宅財形貯蓄だけでなく,一般財形貯蓄や財形年金貯蓄も含むので注意が必要.
住宅ローンの返済方法
住宅ローンの返済方法には,元利均等返済と元金均等返済の2種類がある.
- 元利均等返済:返済額(元金+利息)が一定
- 元金均等返済:元金が一定
住宅ローンの繰上げ返済方法
繰上げ返済の方式には,返済期間短縮型と返済額軽減型の2種類がある.
- 返済期間短縮型:返済額はそのままに期間を短縮
- 返済額軽減型 :返済額を減らし,期間はそのまま
住宅ローンの借り換え
借り換えは,金利の高いローンを一括返済し,金利の低いローンに換えること.ローン手数料などもかかるため考慮に入れる必要あり.
財形住宅貯蓄などの公的ローンへの借り換えはできないので注意が必要.
資金計画に使う6つの係数
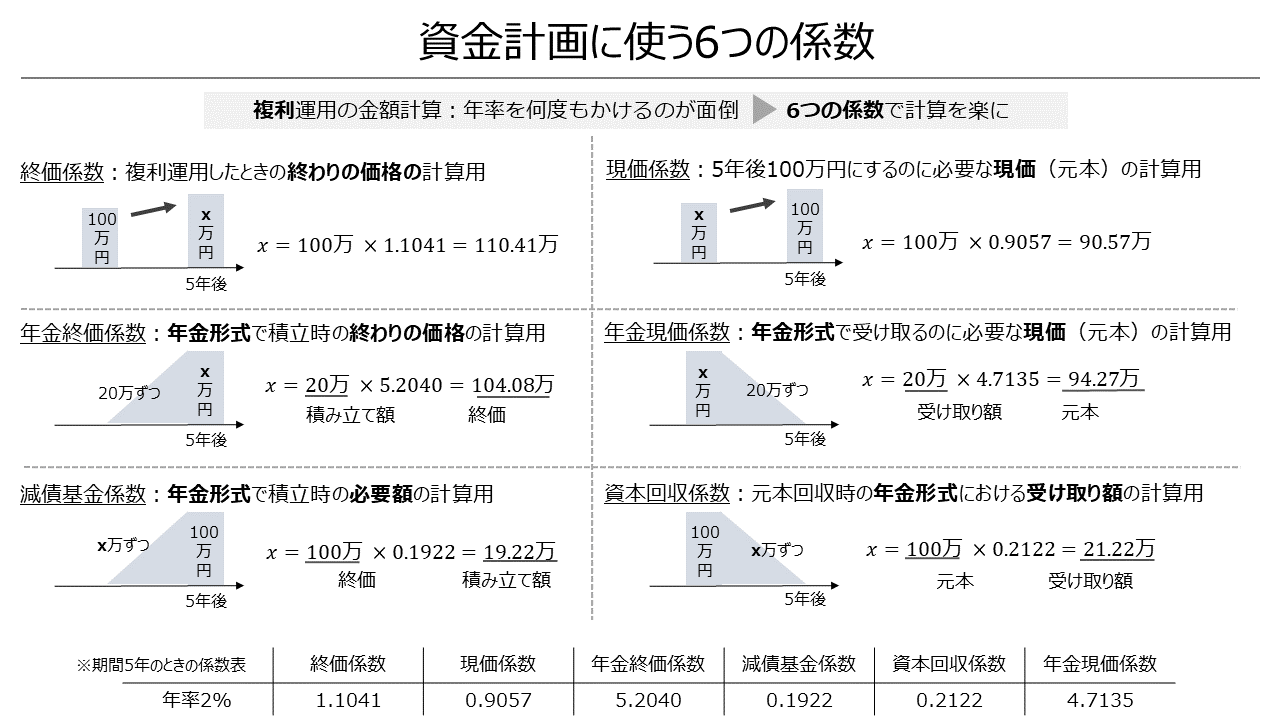
6つの係数
資金計画は複利で運用したときを想定して計画するが,複利なので何度も年率をかけて計算する必要があり,手間になる.
そのときに計算を簡単にしてくれるのが6つの係数である.
終価係数
複利で運用したときの数年後の金額(終価)を求めるときに用いる係数.
(現価)x(終価係数)->(終価)のように,現価から終価を計算する係数と覚えておく.
例:100万円を年利2%で運用したときの5年後の価格
100万×1.1041=110.41万
現価係数
複利で運用するときの数年後100万円にするのに必要な元本(現価)を求めるのに用いる係数.
(終価)x(現価係数)->(現価)のように,終価から現価を計算する係数と覚えておく.
例:年利2%で5年後に100万円を用意するのに必要な金額
100万×0.9057=90.57万
年金終価係数
複利で運用して年金形式で毎年積み立てたとき,一定期間後の金額を求めるのに用いる係数.
(年金積立額)x(年金終価係数)->(終価)のように,年金積立額から終価を計算する係数と覚えておく.
例:年利2%で毎年20万円を5年間積み立てたときの5年後の金額
20万×5.2040=104.08万
年金現価係数
複利で運用しながら年金形式で毎年一定額を受け取りたいとき,必要な元本を求めるのに用いる係数.
(年金受け取り額)x(年金現価係数)->(現価)のように,年金受け取り額から現価を計算する係数と覚えておく.
例:5年間に渡り毎年20万円を受け取りたいときに必要な金額
20万×4.7135=94.27万
減債基金係数
ある期間で一定金額を用意する際の,毎年の積立額を計算するときに用いる係数
(終価)x(減債基金係数)->(毎年の積立額)のように,終価から積立額を計算する係数と覚えておく.
例:年利2%で運用しながら,5年後に100万円用意のに必要な毎年の積立額
100万×0.1922=19.22万
資本回収係数
複利で運用しながら,現在の一定金額を取り崩すときの毎年の受取額の計算に用いる係数
(現価)x(資本回収係数)->(毎年の受取額)のように,現価から受け取り額を計算する係数と覚えておく.
例:100万円を年利2%で運用しながら5年間に渡り取り崩したときの毎年の受取額
100万 ×0.2122=21.22万


