この記事では,数値計算における固有値および固有ベクトルのアルゴリズムについて述べたあと,pythonのサンプルコードで理解を深める.
固有値,固有ベクトル
係数行列$\boldsymbol{A}$ の固有値および固有ベクトルはそれぞれ,次のような同次方程式
$$\boldsymbol{A} \boldsymbol{y} = \lambda \boldsymbol{y}$$
を満たすときの $\lambda$ および,自明解 ($\boldsymbol{y}=\boldsymbol{0}$) でない解 $\boldsymbol{y}$ である.
上記を満たす複数個の固有値と固有ベクトルを一度に表すと
$$\boldsymbol{A} \boldsymbol{M} = \boldsymbol{M} \boldsymbol{D}$$
となる.
$\boldsymbol{M}$ は固有ベクトル,$\boldsymbol{D}$ は対角成分を固有値とする行列である.
$\boldsymbol{A}$ が 2×2 のときで例示すると
$$
\boldsymbol{A} \begin{pmatrix}
y_{11} & y_{12} \\
y_{21} & y_{22}
\end{pmatrix}=
\begin{pmatrix}
y_{11} & y_{12} \\
y_{21} & y_{22}
\end{pmatrix}
\begin{pmatrix}
\lambda_1 & 0 \\
0 & \lambda_2
\end{pmatrix}
$$
である.
固有ベクトルを結合したベクトル $M$ は直交行列であるから,$\boldsymbol{M}^T = \boldsymbol{M}^{-1}$ である.
これを用いて,$\boldsymbol{A} \boldsymbol{M} = \boldsymbol{M} \boldsymbol{D}$ の両辺に左から $\boldsymbol{M}^T$ をかけると
$$\boldsymbol{M}^T \boldsymbol{A} \boldsymbol{M} = \boldsymbol{D}$$
になる.
この方程式の右辺 $\boldsymbol{D}$ は固有値が対角上に並んだ対角行列になっているので,左辺 $\boldsymbol{U}^T \boldsymbol{A} \boldsymbol{U}$ を対角行列となるような $U$ を求めれば,そのような $\boldsymbol{U}$ から固有ベクトル,$\boldsymbol{U}^T \boldsymbol{A} \boldsymbol{U}$ から固有値を求められる.
ヤコビ法
上記のように,$\boldsymbol{U}^T \boldsymbol{A} \boldsymbol{U}$ を対角行列となるような $M$ を求めることで固有値と固有ベクトルが求められることが分かった.
計算機においては,これを行うアルゴリズムとしてヤコビ法がある.
ヤコビ法は,行列$\boldsymbol{A}$の非対角要素の1つのみを 0 にする直交行列$\boldsymbol{R}_i~(i=1,2,\cdots)$をかけ,この操作を繰り返し行う.
0 にする非対角要素は行列 $\boldsymbol{A}$ の最大値の要素とする.
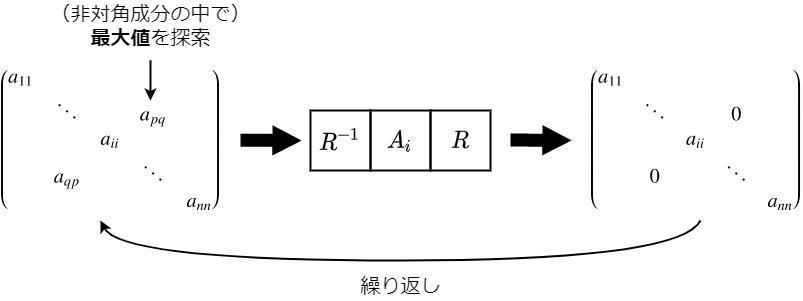
$n$ 回繰り返したとき,
$$
\begin{aligned}
\boldsymbol{A_n} &= \boldsymbol{R}_n^T \cdots \boldsymbol{R}_2^T\boldsymbol{R}_1^T \boldsymbol{A} \boldsymbol{R}_1 \boldsymbol{R}_2 \cdots \boldsymbol{R}_n \\
\boldsymbol{A_n} &= (\boldsymbol{R}_1 \boldsymbol{R}_2 \cdots \boldsymbol{R}_n)^T \boldsymbol{A} (\boldsymbol{R}_1 \boldsymbol{R}_2 \cdots \boldsymbol{R}_n)
\end{aligned}
$$
$\boldsymbol{D} = \boldsymbol{U}^T \boldsymbol{A} \boldsymbol{U}$ と比較すると,
$$
\begin{aligned}
\boldsymbol{U} \leftarrow \boldsymbol{U}_n &= \boldsymbol{R}_1 \boldsymbol{R}_2 \cdots \boldsymbol{R}_n \\
\boldsymbol{D} \leftarrow \boldsymbol{A}_n &= (\boldsymbol{R}_1 \boldsymbol{R}_2 \cdots \boldsymbol{R}_n)^T \boldsymbol{A} (\boldsymbol{R}_1 \boldsymbol{R}_2 \cdots \boldsymbol{R}_n)
\end{aligned}
$$
となるので,
- 演算後の$\boldsymbol{A}_n$ -> 固有値
- 演算後の$\boldsymbol{U}_n$ -> 固有ベクトル
として求められる.
非対角要素の1つを0にする直交行列
あとは,行列$\boldsymbol{A}$の非対角要素の1つのみを 0 にする直交行列$\boldsymbol{R}_i~(i=1,2,\cdots)$ がどのような行列であるかである.
この行列には次に示すものを用いる.
この行列はギブンス回転行列として知られる.
$$
\boldsymbol{R} = \begin{pmatrix}
1 & \cdots & 0 & \cdots & 0 & \cdots & 0\\
\vdots & \ddots & \vdots & & \vdots & & 0\\
0 & \cdots & \cos{\theta} & \cdots & \sin{\theta} & \cdots & 0\\
\vdots & & \vdots & \ddots & \vdots & & 0\\
0 & \cdots & -\sin{\theta} & \cdots & \cos{\theta} & \cdots & 0\\
\vdots & & \vdots & & \vdots & \ddots & 0\\
0 & \cdots & 0 & \cdots & 0 & \cdots & 1
\end{pmatrix}
$$
この行列$\boldsymbol{R}$ は,$p, q$行および$p,q$ 列が交差する要素が $\sin{\theta}$ と $\cos{\theta}$ で構成される要素となっており,そのほかの要素は単位行列と同様である.
この行列は$\theta$の値に関わらず $\boldsymbol{R}^T \boldsymbol{R}=I$ となるので,$\boldsymbol{R}$ は直交行列である.
$\theta$ の値の決め方
あとは,$\theta$ の具体的な数値であるが,これは $\boldsymbol{B}=\boldsymbol{R}^{-1} \boldsymbol{A} \boldsymbol{R}$ の要素 $b_{ij}$ とすると,$b_{pq}$ を 0 にするように設定する.
$b_{ij}$ の一部を書き下すと
$$
\begin{aligned}
b_{pp} &= a_{pp} \cos^2 \theta + a_{qq} \sin^2 \theta – 2a_{pq} \sin \theta \cos \theta \\
b_{qq} &= a_{pp} \sin^2 \theta + a_{qq} \cos^2 \theta – 2a_{pq} \sin \theta \cos \theta \\
b_{pq} &= (a_{pp} – a_{qq}) \sin \theta \cos \theta + a_{pq} (\cos^2 \theta – \sin^2 \theta) \\
&= \dfrac{1}{2}(a_{pp} – a_{qq} \sin{2 \theta}) + a_{pq} \cos{2 \theta} \\
b_{qp} &= b_{pq}
\end{aligned}
$$
となる.
$\theta$ は任意の値を取れるので,$b_{pq}$ を 0 にする $\theta_0$ の条件は
$$
\begin{aligned}
b_{pq} &= \dfrac{1}{2}(a_{pp} – a_{qq} \sin{2 \theta_0}) + a_{pq} \cos{2 \theta_0} = 0 \nonumber \\
\leftrightarrow & ~ r \sin{(2 \theta + \phi)} = 0 \nonumber \\
\leftrightarrow & ~ 2 \theta + \phi = 0, \pi, 2\pi, \cdots
\end{aligned}
$$
計算には三角関数の合成を用いた.
ここで,$r, \phi$ については
$$
\begin{aligned}
\tan \phi &= \frac{2 a_{pq}}{a_{pp}-a_{qq}} \\
r &= \sqrt{\frac{1}{4} (a_{pp} – a_{qp})^2 + {a_{pq}}^2} \\
\end{aligned}
$$
である.
$\theta$ と $\phi$ の関係から $\tan 2\theta = -\tan \phi$ なので,
$$
\begin{aligned}
\tan 2\theta &= – \frac{2 a_{pq}}{a_{pp}-a_{qq}} \\
\leftrightarrow \sin 2\theta &= \frac{a_{pq}}{r}, ~ \cos 2\theta = – \frac{a_{pp} – a_{qq}}{r}
\end{aligned}
$$
という条件に書き換えられる.
ここで,図のように$\sin 2\theta$ の符号で場合分けし,
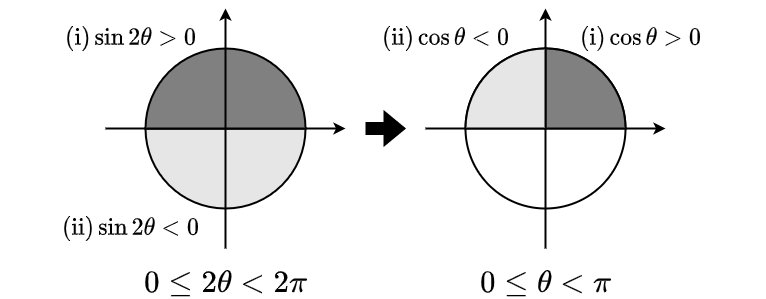
半角の公式を用いれば,$\sin \theta$ および $\cos \theta$ が得られる.
$$
\begin{aligned}
\sin \theta &= \sqrt{\frac{1}{2} + \frac{a_{pp} – a_{qq}}{4r}} \\
\cos \theta &= {\rm sgn}(a_{pq}) \cdot \sqrt{\frac{1}{2} – \frac{a_{pp} – a_{qq}}{4r}}
\end{aligned}
$$
これらを代入した $\boldsymbol{R}$ で繰り返し対角化を行っていくことで,固有値と固有ベクトルを求められる.
Python コード
上記で説明したヤコビ法のPythonコードを次に示す.
import numpy as np
## ------ params ------ ##
A_mat = np.array([
[ 5.0000, -1.4142, 0.0000],
[-1.4142, 1.5000, -0.4083],
[-0.0000, -0.4083, -0.3333]
])
eps = 1e-5
dim = A_mat.shape[0]
## ------ main ------ ##
Ai_mat = A_mat
eigen_mat = np.identity(dim)
while True:
## eliminate diagonal elements
Ai_diag0_mat = np.abs(Ai_mat) #
Ai_diag0_mat[range(dim), range(dim)] = 0
## search the maximum element in [Ai]
index = np.argmax(Ai_diag0_mat)
index = np.unravel_index(index, Ai_mat.shape)
## convergence judgement
#print(Ai_diag0_mat[index])
if Ai_diag0_mat[index] < eps:
break
## calculate sin cos
p = index[0]
q = index[1]
app = Ai_mat[p, p]
aqq = Ai_mat[q, q]
apq = Ai_mat[p, q]
radius = np.sqrt(((app-aqq)**2) / 4 + apq**2)
cos = np.sign(apq)*np.sqrt(0.5 - (app-aqq) / (4*radius))
sin = np.sqrt(0.5 + (app-aqq) / (4*radius))
## calculate [R]
R_mat = np.identity(Ai_mat.shape[0])
R_mat[p, p] = cos
R_mat[p, q] = sin
R_mat[q, p] = -sin
R_mat[q, q] = cos
## diagonalize [Ai] : calculate [R^T][Ai][R]
Ai_mat = np.linalg.multi_dot([R_mat.T, Ai_mat, R_mat])
eigen_mat = np.dot(eigen_mat, R_mat)
print('eigen value')
print(Ai_mat)
print('eigen vector')
print(eigen_mat)このコードにより,次のような出力が得られる.
eigen value
[[ 1.10288688e+00 -4.51031917e-14 3.15398829e-09]
[-4.51027999e-14 -4.39370004e-01 -6.23993818e-06]
[ 3.15398847e-09 -6.23993818e-06 5.50318312e+00]]
eigen vector
[[ 0.32955317 -0.0652321 -0.94188082]
[ 0.90815017 -0.25090326 0.33512808]
[-0.25818208 -0.96581175 -0.02344542]]また,numpy には固有値と固有ベクトルを計算する関数が用意されており,この出力と結果が一致することから,正確に計算できていることが確認できる.
w, v = np.linalg.eig(A_mat)
print(w)
print(v)[ 5.50318312 1.10288688 -0.43937 ]
[[ 0.94188075 0.32955317 0.06523309]
[-0.33512834 0.90815017 0.25090291]
[ 0.02344441 -0.25818208 0.96581177]]まとめ
固有値と固有ベクトルを数値計算するアルゴリズムとしてヤコビ法を紹介した.
ヤコビ法は,対角化演算 $\boldsymbol{B}=\boldsymbol{R}^{-1} \boldsymbol{A} \boldsymbol{R}$ をしたときの1つの非対角要素を 0 にすることを繰り返し行うことで,対角化を行って,固有値と固有ベクトルを計算する手法である.
$\boldsymbol{R}$ には,ギブンス変換行列の $\theta$ を適切に設定したものが使用される.
参考
[1] 三井田 惇郎,須田 宇宙,数値計算法[第2版],森北出版,2014




