2リンクロボットアームの逆運動学

概要

2リンクロボットアームの各アーム長さと角度を図のように定義する．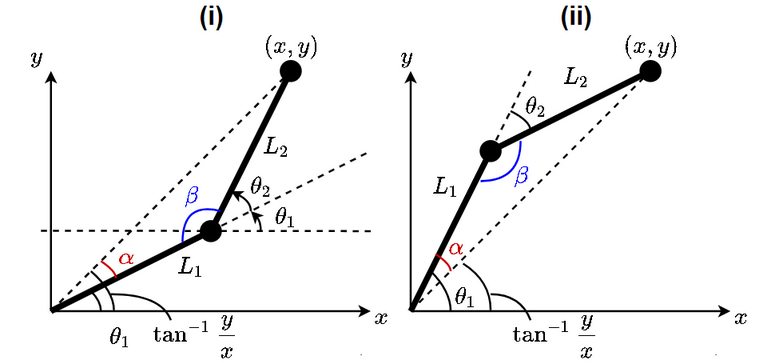

解は図のような2種類あり，それぞれ次のようになる．

(i)の場合，
$$
\begin{aligned}
\theta_1 = \tan^{-1} \frac{y}{x} – \cos^{-1} \frac{{L_1}^2 – {L_2}^2 + x^2 + y^2}{2 L_1 \sqrt{x^2 + y^2}} \\
\theta_2 = \pi – \cos^{-1}\frac{{L_1}^2 + {L_2}^2 – x^2 – y^2}{2 L_1 L_2}
\end{aligned}
$$

(ii)の場合，
$$
\begin{aligned}
\theta_1 = \tan^{-1} \frac{y}{x} + \cos^{-1} \frac{{L_1}^2 – {L_2}^2 + x^2 + y^2}{2 L_1 \sqrt{x^2 + y^2}} \\
\theta_2 = \cos^{-1}\frac{{L_1}^2 + {L_2}^2 – x^2 – y^2}{2 L_1 L_2} -\pi
\end{aligned}
$$

余弦定理を用いた逆運動学の導出方法

式の導出

図の$\alpha, \beta$に対して，それぞれ余弦定理を適用し，$\alpha, \beta$について整理する．

$\alpha$については，
$$
\begin{aligned}
{L_2}^2 &= {L_1}^2 + x^2+ y^2-2L_1\sqrt{x^2+y^2} \cos{\alpha} \\
\cos \alpha &= \frac{{L_1}^2 -{L_2}^2 + x^2+ y^2}{2L_1 \sqrt{x^2+y^2}}
\end{aligned}
$$
$\alpha > 0$とすると，$\theta_1$は，
$$
\begin{aligned}
\theta_1 \mp \alpha &= \tan^{-1} \frac{y}{x} \\
\theta_1 &= \tan^{-1} \frac{y}{x} \pm \cos^{-1} \frac{{L_1}^2 -{L_2}^2 + x^2+ y^2}{2L_1 \sqrt{x^2+y^2}}
\end{aligned}
$$
と求まる．

$\beta$については，
$$
\begin{aligned}
x^2 + y^2 &= {L_1}^2 + {L_2}^2 -2L_1 L_2 \cos{\beta} \\
\cos \beta&= \frac{{L_1}^2 + {L_2}^2 – x^2- y^2}{2L_1 L_2 } \\
\end{aligned}
$$
$\beta > 0$とすると，$\theta_1$は，
$$
\begin{aligned}
\theta_2 &= \pm (\pi – \beta) \\
&= \pm \left\{ \pi – \cos^{-1} \frac{{L_1}^2 + {L_2}^2 – x^2- y^2}{2L_1 L_2 } \right\}
\end{aligned}
$$

が成り立つ．