下のような別の角度からの画像2枚を貼り合わせることを目指します.
opencvを用いると簡単にできるようですが,今回は理解を深めるためにpythonでopencvを使わず書きます.
2枚の画像を貼り合わせる場合,画像のどことどこが対応しているかが数点必要となるので,今回対応点ははあらかじめ手動で与えることとします.
以下では,左の画像1を右の画像2に貼り合わせる方法について書いています.
対応点は画像の赤で示した点としました.


ホモグラフィ変換(Homography Transform)
ホモグラフィ変換とは射影変換によって平面を異なる平面に射影すること
ホモグラフィ行列
画像1の座標を\( (x,y)^{\rm T} \),画像2の座標を\( (x’,y’)^{\rm T} \)と置くと,
\begin{align} \begin{pmatrix} x’ \\ y’ \\ 1 \end{pmatrix} = \begin{pmatrix} h_{11} & h_{12} & h_{13} \\ h_{21} & h_{22} & h_{23} \\ h_{31} & h_{32} & h_{33} \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{align}
のように表せる.
\( h_{11} \sim h_{33} \)で表される行列はホモグラフィ行列である.
このホモグラフィ行列を対応点の座標から求めることで変換前と変換後の座標関係が決まる.
\begin{align} \textbf{h}= \begin{pmatrix} h_{11} & h_{12} & h_{13} & h_{21} & h_{22} & h_{23} & h_{31} & h_{32} & h_{33} \end{pmatrix} \end{align}
と表しhについての式に変換すると
\begin{align} \begin{pmatrix} x & y & 1 & 0 & 0 & 0 & -xx’ & -yx’ & -x’ \\ 0 & 0 & 0 & x & y & 1 & -xy’ & -yy’ & -y’ \end{pmatrix} \textbf{h} = \textbf{0} \end{align}
2つの画像の対応点が既知のとき,変数9個の斉次方程式であるので上記の式が4つ必要となる.
よって,hを求めるためには最低4組の対応点\( (x_i, y_i)^{\rm T} \),\( (x_i’, y_i’)^{\rm T} \)が必要である.
これらをまとめると,
\begin{align} \begin{pmatrix} x_1 & y_1 & 1 & 0 & 0 & 0 & -x_1 x’_1 & -y_1 x’_1 & -x’_1 \\ x_2 & y_2 & 1 & 0 & 0 & 0 & -x_2 x’_2 & -y_2 x’_2 & -x’_2 \\ x_3 & y_3 & 1 & 0 & 0 & 0 & -x_3 x’_3 & -y_3 x’_3 & -x’_3 \\ x_4 & y_4 & 1 & 0 & 0 & 0 & -x_4 x’_4 & -y_4 x’_4 & -x’_4 \\ 0 & 0 & 0 & x_1 & y_1 & 1 & -x_1 y’_1 & -y_1 y’_1 & -y’_1 \\ 0 & 0 & 0 & x_2 & y_2 & 1 & -x_2 y’_2 & -y_2 y’_2 & -y’_2 \\ 0 & 0 & 0 & x_3 & y_3 & 1 & -x_3 y’_3 & -y_3 y’_3 & -y’_3 \\ 0 & 0 & 0 & x_4 & y_4 & 1 & -x_4 y’_4 & -y_4 y’_4 & -y’_4 \\ \end{pmatrix} \textbf{h} = \textbf{0} \end{align}
が成立し,この方程式を解くことでホモグラフィ行列 \( \textbf{h} \) が求まる.
ホモグラフィ行列の導出方法
この方程式の自明解( \( h = 0\) )でない解を求めるために,上式の行列\( A \)を特異値分解する.
特異値分解によって\( A= U \Sigma V^{\rm T} \)とできたとき,hの最小二乗解はVの最後の列ベクトルである\( \textbf{v}_9 \)を求めることで得られる.
なぜ上記で求められるか
hの最小二乗解すなわち\( ||A\textbf{h}||^2 \)を最小にする解を考える.
特異値分解によって得られる\( U, V \)は直交行列であるので, \begin{align} ||A \textbf{h}|| = ||U \Sigma V^T \textbf{h} || = ||\Sigma V^{\rm T} \textbf{h}|| = ||\Sigma \textbf{y} || \end{align}
が成立する.また\(\Sigma \)は, \begin{align} \Sigma = \begin{pmatrix} \sigma_1 & & & & & 0 \\ & \sigma_2 & & & & \\ & & \ddots & & & \vdots \\ & & & \sigma_7 & & \\ & & & & \sigma_8 & 0 \end{pmatrix} \end{align}
のように表せるので\( \Sigma \textbf{y} = 0 \)を満たす\( \textbf{y} \)は \begin{align} \textbf{y} = V^{\rm T} \textbf{h} = (0, 0, \cdots, 0, 1)^{\rm T} \end{align}
となる.\( V^{\rm T} \)は直交行列より,\( V^{\rm T} = V^{\rm -1} \)が成立するから,
\begin{align} \textbf{h} = V \textbf{y} = V (0, 0, \cdots, 0, 1)^{\rm T} = \textbf{v}_9 \end{align}
補間
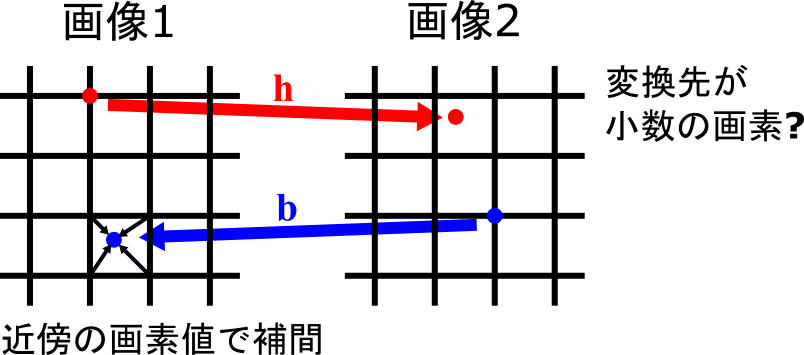
上記よりホモグラフィ行列hが導出でき,画像1から画像2への変換できる.
しかし,下の図のように画像1から画像2への変換結果は小数であるため,画素値をどう決定するかが問題で四捨五入してしまうと変換後の画素が重なることや埋まらない画素が存在してしまう.
ここで,hの逆変換であるbを考える.
画像2のすべての画素において逆変換して,得られた小数座標の画素値を近傍の画素値を用いて補間することで画像2の格子点(整数座標)の画素値を決定する.
補間方法は共1次補間によって行った.
コード
上で説明したような処理は以下のようにpythonで実装できる.
import numpy as np
import pathlib
import matplotlib.pyplot as plt
import matplotlib.ticker as ptick
from PIL import Image
img1_path = pathlib.Path('./data/homography_picture1.jpg')
img2_path = pathlib.Path('./data/homography_picture2.jpg')
output_path = pathlib.Path('./data/result.jpg')
img1 = np.array(Image.open(img1_path))
img2 = np.array(Image.open(img2_path))
result = np.zeros(img1.shape).astype(np.uint8)
print(img1.shape)
# corresponding point
# 4point ver.
x1 = np.array([416, 842, 681, 34])
y1 = np.array([602, 41, 270, 182])
x2 = np.array([289, 1063, 730, 336])
y2 = np.array([477, 294, 387, 66])
# 5point ver.
x1 = np.array([416, 842, 681, 34, 315])
y1 = np.array([602, 41, 270, 182, 206])
x2 = np.array([289, 1063, 730, 336, 498])
y2 = np.array([477, 294, 387, 66, 182])
for i in range(np.size(x1)):
# line1 of A
A1 = np.zeros(9)
A2 = np.zeros(9)
A1[0] = x1[i]
A1[1] = y1[i]
A1[2] = 1
A1[3:5] = 0
A1[6] = -1 * x1[i] * x2[i]
A1[7] = -1 * y1[i] * x2[i]
A1[8] = -1 * x2[i]
A1 = A1.reshape([1, np.size(A1)])
#line2 of A
A2[0:2] = 0
A2[3] = x1[i]
A2[4] = y1[i]
A2[5] = 1
A2[6] = -1 * x1[i] * y2[i]
A2[7] = -1 * y1[i] * y2[i]
A2[8] = -1 * y2[i]
A2 = A2.reshape([1, np.size(A2)])
_A = np.concatenate([A1, A2], 0)
if i == 0:
A = _A
else:
A = np.concatenate([A, _A], 0)
# homography param
# singular value decomposition
U, S, V = np.linalg.svd(A)
H = V[8] / V[8, 8]
H = H.reshape(3, 3)
H12 = H[0:2, :]
H3 = H[2, :]
# get inverse transform of H
B = np.linalg.inv(H)
B = B / B[2, 2]
B12 = B[0:2, :]
B3 = B[2, :]
# coodinate transform
z = np.ones(img2.shape[0] * img2.shape[1])
z = z.reshape([1, np.size(z)])
for i in range(img2.shape[0]):
_x2 = np.arange(0, img2.shape[1], 1)
_y2 = np.full(img2.shape[1], i)
_x2 = _x2.reshape([1, np.size(_x2)])
_y2 = _y2.reshape([1, np.size(_y2)])
if i == 0:
x2 = _x2
y2 = _y2
else:
x2 = np.concatenate([x2, _x2], 1)
y2 = np.concatenate([y2, _y2], 1)
points2 = np.concatenate([x2, y2], 0)
points2 = np.concatenate([points2, z], 0)
s = np.dot(B3, points2)
points1 = np.dot(B12, points2) / s
x1 = points1[0, :].reshape([img2.shape[0], img2.shape[1]])
y1 = points1[1, :].reshape([img2.shape[0], img2.shape[1]])
# linear interpolation
xf1 = np.floor(x1).astype(int)
yf1 = np.floor(y1).astype(int)
for i in range(img2.shape[0]):
for j in range(img2.shape[1]):
if x1[i, j] > 0 and x1[i, j] < img2.shape[1] - 1:
if y1[i, j] > 0 and y1[i, j] < img2.shape[0] - 1:
result[i, j, :] = \
(x1[i, j] - xf1[i, j]) * (y1[i, j] - yf1[i, j]) * img1[yf1[i, j], xf1[i, j], :] + \
(x1[i, j] - xf1[i, j]) * (yf1[i, j] - y1[i, j] + 1) * img1[yf1[i, j] + 1, xf1[i, j], :] + \
(xf1[i, j] - x1[i, j] + 1) * (y1[i, j] - yf1[i, j]) * img1[yf1[i, j], xf1[i, j] + 1, :] + \
(xf1[i, j] - x1[i, j] + 1) * (yf1[i, j] - y1[i, j] + 1) * img1[yf1[i, j] + 1, xf1[i, j] + 1, :]
# save image
result = result.astype(np.uint8)
result_img = Image.fromarray(result)
result_img.save(output_path)
